
Frozen Lake meets Value Iteration
The Frozen Lake
This lake has a 4×4 grid of total 16 states.
# Frozen Lake Gridworld:
It is highly stochastic environment (33.33% action success, 66.66% split evenly in right angles)
It contains 4×4 grid, 16 states (0-15)
The agent gets +1 for landing in state 15 (right bottom corner) 0 otherwise
The states 5, 7, 11, and 12 are holes, agents die in holes, no penalty, just end of episode.
The state 15 is the goal, reaching it ends the episode too
The agent starts in state 0 (top left corner)
There are four actions that an agent can take: left (0), down (1), right (2), up (3).

Defining Frozen Lake with dictionary in Python
# Frozen Lake Gridworld:
# highly stochastic environment (33.33% action success, 66.66% split evenly in right angles)
# 4x4 grid, 16 states 0-15
# +1 for landing in state 15 (top bottom corner) 0 otherwise
# states 5, 7, 11, and 12 are holes, agents die in holes, no penalty, just end of episode
# state 15 is the goal, reaching it ends the episode too
# agent starts in state 0 (top left corner)
# actions left (0), down (1), right (2), up (3)
P = {
0: {
0: [(0.6666666666666666, 0, 0.0, False),
(0.3333333333333333, 4, 0.0, False)
],
1: [(0.3333333333333333, 0, 0.0, False),
(0.3333333333333333, 4, 0.0, False),
(0.3333333333333333, 1, 0.0, False)
],
2: [(0.3333333333333333, 4, 0.0, False),
(0.3333333333333333, 1, 0.0, False),
(0.3333333333333333, 0, 0.0, False)
],
3: [(0.3333333333333333, 1, 0.0, False),
(0.6666666666666666, 0, 0.0, False)
]
},
1: {
0: [(0.3333333333333333, 1, 0.0, False),
(0.3333333333333333, 0, 0.0, False),
(0.3333333333333333, 5, 0.0, True)
],
1: [(0.3333333333333333, 0, 0.0, False),
(0.3333333333333333, 5, 0.0, True),
(0.3333333333333333, 2, 0.0, False)
],
2: [(0.3333333333333333, 5, 0.0, True),
(0.3333333333333333, 2, 0.0, False),
(0.3333333333333333, 1, 0.0, False)
],
3: [(0.3333333333333333, 2, 0.0, False),
(0.3333333333333333, 1, 0.0, False),
(0.3333333333333333, 0, 0.0, False)
]
},
2: {
0: [(0.3333333333333333, 2, 0.0, False),
(0.3333333333333333, 1, 0.0, False),
(0.3333333333333333, 6, 0.0, False)
],
1: [(0.3333333333333333, 1, 0.0, False),
(0.3333333333333333, 6, 0.0, False),
(0.3333333333333333, 3, 0.0, False)
],
2: [(0.3333333333333333, 6, 0.0, False),
(0.3333333333333333, 3, 0.0, False),
(0.3333333333333333, 2, 0.0, False)
],
3: [(0.3333333333333333, 3, 0.0, False),
(0.3333333333333333, 2, 0.0, False),
(0.3333333333333333, 1, 0.0, False)
]
},
3: {
0: [(0.3333333333333333, 3, 0.0, False),
(0.3333333333333333, 2, 0.0, False),
(0.3333333333333333, 7, 0.0, True)
],
1: [(0.3333333333333333, 2, 0.0, False),
(0.3333333333333333, 7, 0.0, True),
(0.3333333333333333, 3, 0.0, False)
],
2: [(0.3333333333333333, 7, 0.0, True),
(0.6666666666666666, 3, 0.0, False)
],
3: [(0.6666666666666666, 3, 0.0, False),
(0.3333333333333333, 2, 0.0, False)
]
},
4: {
0: [(0.3333333333333333, 0, 0.0, False),
(0.3333333333333333, 4, 0.0, False),
(0.3333333333333333, 8, 0.0, False)
],
1: [(0.3333333333333333, 4, 0.0, False),
(0.3333333333333333, 8, 0.0, False),
(0.3333333333333333, 5, 0.0, True)
],
2: [(0.3333333333333333, 8, 0.0, False),
(0.3333333333333333, 5, 0.0, True),
(0.3333333333333333, 0, 0.0, False)
],
3: [(0.3333333333333333, 5, 0.0, True),
(0.3333333333333333, 0, 0.0, False),
(0.3333333333333333, 4, 0.0, False)
]
},
5: {
0: [(1.0, 5, 0, True)],
1: [(1.0, 5, 0, True)],
2: [(1.0, 5, 0, True)],
3: [(1.0, 5, 0, True)]
},
6: {
0: [(0.3333333333333333, 2, 0.0, False),
(0.3333333333333333, 5, 0.0, True),
(0.3333333333333333, 10, 0.0, False)
],
1: [(0.3333333333333333, 5, 0.0, True),
(0.3333333333333333, 10, 0.0, False),
(0.3333333333333333, 7, 0.0, True)
],
2: [(0.3333333333333333, 10, 0.0, False),
(0.3333333333333333, 7, 0.0, True),
(0.3333333333333333, 2, 0.0, False)
],
3: [(0.3333333333333333, 7, 0.0, True),
(0.3333333333333333, 2, 0.0, False),
(0.3333333333333333, 5, 0.0, True)
]
},
7: {
0: [(1.0, 7, 0, True)],
1: [(1.0, 7, 0, True)],
2: [(1.0, 7, 0, True)],
3: [(1.0, 7, 0, True)]
},
8: {
0: [(0.3333333333333333, 4, 0.0, False),
(0.3333333333333333, 8, 0.0, False),
(0.3333333333333333, 12, 0.0, True)
],
1: [(0.3333333333333333, 8, 0.0, False),
(0.3333333333333333, 12, 0.0, True),
(0.3333333333333333, 9, 0.0, False)
],
2: [(0.3333333333333333, 12, 0.0, True),
(0.3333333333333333, 9, 0.0, False),
(0.3333333333333333, 4, 0.0, False)
],
3: [(0.3333333333333333, 9, 0.0, False),
(0.3333333333333333, 4, 0.0, False),
(0.3333333333333333, 8, 0.0, False)
]
},
9: {
0: [(0.3333333333333333, 5, 0.0, True),
(0.3333333333333333, 8, 0.0, False),
(0.3333333333333333, 13, 0.0, False)
],
1: [(0.3333333333333333, 8, 0.0, False),
(0.3333333333333333, 13, 0.0, False),
(0.3333333333333333, 10, 0.0, False)
],
2: [(0.3333333333333333, 13, 0.0, False),
(0.3333333333333333, 10, 0.0, False),
(0.3333333333333333, 5, 0.0, True)
],
3: [(0.3333333333333333, 10, 0.0, False),
(0.3333333333333333, 5, 0.0, True),
(0.3333333333333333, 8, 0.0, False)
]
},
10: {
0: [(0.3333333333333333, 6, 0.0, False),
(0.3333333333333333, 9, 0.0, False),
(0.3333333333333333, 14, 0.0, False)
],
1: [(0.3333333333333333, 9, 0.0, False),
(0.3333333333333333, 14, 0.0, False),
(0.3333333333333333, 11, 0.0, True)
],
2: [(0.3333333333333333, 14, 0.0, False),
(0.3333333333333333, 11, 0.0, True),
(0.3333333333333333, 6, 0.0, False)
],
3: [(0.3333333333333333, 11, 0.0, True),
(0.3333333333333333, 6, 0.0, False),
(0.3333333333333333, 9, 0.0, False)
]
},
11: {
0: [(1.0, 11, 0, True)],
1: [(1.0, 11, 0, True)],
2: [(1.0, 11, 0, True)],
3: [(1.0, 11, 0, True)]
},
12: {
0: [(1.0, 12, 0, True)],
1: [(1.0, 12, 0, True)],
2: [(1.0, 12, 0, True)],
3: [(1.0, 12, 0, True)]
},
13: {
0: [(0.3333333333333333, 9, 0.0, False),
(0.3333333333333333, 12, 0.0, True),
(0.3333333333333333, 13, 0.0, False)
],
1: [(0.3333333333333333, 12, 0.0, True),
(0.3333333333333333, 13, 0.0, False),
(0.3333333333333333, 14, 0.0, False)
],
2: [(0.3333333333333333, 13, 0.0, False),
(0.3333333333333333, 14, 0.0, False),
(0.3333333333333333, 9, 0.0, False)
],
3: [(0.3333333333333333, 14, 0.0, False),
(0.3333333333333333, 9, 0.0, False),
(0.3333333333333333, 12, 0.0, True)
]
},
14: {
0: [(0.3333333333333333, 10, 0.0, False),
(0.3333333333333333, 13, 0.0, False),
(0.3333333333333333, 14, 0.0, False)
],
1: [(0.3333333333333333, 13, 0.0, False),
(0.3333333333333333, 14, 0.0, False),
(0.3333333333333333, 15, 1.0, True)
],
2: [(0.3333333333333333, 14, 0.0, False),
(0.3333333333333333, 15, 1.0, True),
(0.3333333333333333, 10, 0.0, False)
],
3: [(0.3333333333333333, 15, 1.0, True),
(0.3333333333333333, 10, 0.0, False),
(0.3333333333333333, 13, 0.0, False)
]
},
15: {
0: [(1.0, 15, 0, True)],
1: [(1.0, 15, 0, True)],
2: [(1.0, 15, 0, True)],
3: [(1.0, 15, 0, True)]
}
}Testing a Policy
Policy defines the action to be taken in a particular state.
Let us evaluate the following policy.
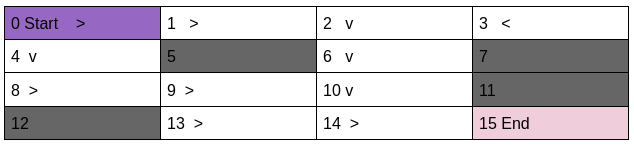
We will see in how many episodes out of 10000, above policy will lead us to our goal.
Code Defining Our Policy
go_get_it_policy = [[2,2,1,0,
1,0,1,0,
2,2,1,0,
0,2,2,0]]Code for Policy Evaluation i.e calculation of win percentage
def policy_testing(P,policy):
frozen_lake_policy_reshaped = policy
win=0
loss = 0
episodes = 1000
#The following algorithm works like
#1. Start from start position (State 0)
#2. Take action according to the policy
#3. The action might take the agent to next state or leave in the current state
#4. Repeat 2 until the agent reaches one of the Holes or reach the goal
#5. If the agent reaches the goal print"We won": end of episode
#6. If the agent fall in one of the holes print "We fucked up": end of episode
win=0
loss = 0
episodes = 10000
for i in range(episodes):
#start
direction = frozen_lake_policy_reshaped[0][0]
#print(direction)
entries = len(P[0][direction])
#print("entries :",entries)
prob_list = []
next_states = []
for entry in range(entries):
#print("Probability")
#print(P[0][direction][entry][0])
#Listing probability of reaching next state for given direction
prob_list.append(P[0][direction][entry][0]*100)
#print("next state")
#print(P[0][direction][entry][1])
#Listing of next state for given direction
next_states.append(P[0][direction][entry][1])
#Selection of next state according to probability
new_next_state = random.choices(next_states, weights=prob_list)[0]
#print("next_state: ",new_next_state)
#print(P[new_next_state][direction][entry][3])
#print("........................\n")
while((P[new_next_state][0][0][3] == False) or (P[new_next_state][0][0][0]!=1)):
#The while loop continues unless any terminal state is reached
#print("current_state: ",new_next_state)
direction = frozen_lake_policy_reshaped[0][new_next_state]
#print("Direction: ",direction)
entries = len(P[new_next_state][direction])
prob_list = []
next_states = []
for entry in range(entries):
#print("next state")
#print(P[new_next_state][direction][entry][1])
next_states.append(P[new_next_state][direction][entry][1])
#print("Probability")
#print(P[new_next_state][direction][entry][0])
prob_list.append(P[new_next_state][direction][entry][0]*100)
new_next_state = random.choices(next_states, weights=prob_list)[0]
#print("next_state: ",new_next_state)
#print(P[new_next_state][0][0][3])
#print(P[new_next_state][0][0][0])
#print(".....................")
if(new_next_state == 15):
win = win+1
#print("we won")
break
elif(new_next_state==5 or new_next_state==7 or new_next_state==11 or new_next_state==12):
loss = loss+1
#print("we fucked up")
break
else:
continue
#print(P[new_next_state][direction][entry][3])
win_percentage = (win/episodes)*100
return win_percentagego_get_it_policy = [[2,2,1,0,
1,0,1,0,
2,2,1,0,
0,2,2,0]]
print(policy_testing(P,go_get_it_policy))3.1%
This policy has winning rate of 3.1%
Can we do better?
One way to come up with the best policy is the value iteration or Greedily greedifying policies.
Let us start with the always left policy.
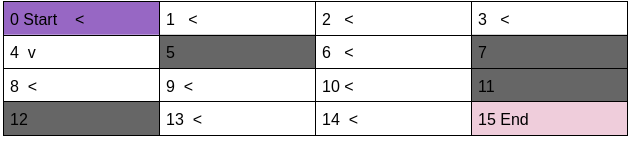
always_left_policy = [[0,0,0,0,
0,0,0,0,
0,0,0,0,
0,0,0,0]]
print(policy_testing(P,all_left_policy))This policy has win rate of 0%
We will start with the value of all states being 0.
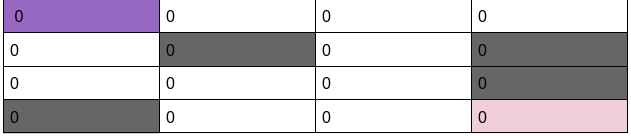
We will update the value for all the actions iteratively.
Value = Sum of all(Probability of reaching next state on taking particular action x (max value of next state + reward))

Let us manually calculate the values
Iteration I
For state 0:
For action 0 (i.e taking Left)
V(s’=0/a=0) = 0.66(0+0) = 0
V(s’=4/a=0) = 0.33(0+0) = 0
V(a=0) = 0
For action 1 (i.e going down)
V(s’=0/a=1) = 0.33(0+0) = 0
V(s’=1/a=1) = 0.33(0+0) = 0
V(s’=4/a=1) = 0.33(0+0) = 0
V(a=1) = 0
For action 2 (i.e taking Right)
V(s’=0/a=2) = 0.33(0+0) = 0
V(s’=1/a=2) = 0.33(0+0) = 0
V(s’=4/a=2) = 0.33(0+0) = 0
V(a=2) = 0
For action 3 (i.e going Up)
V(s’=0/a=3) = 0.66(0+0) = 0
V(s’=1/a=3) = 0.33(0+0) = 0
V(a=3) = 0
In the first iteration we get value = 0 in all states for all actions except for state 14.
For state 14:
For action 0 (i.e taking Left)
V(s’=13/a=0) = 0.33(0+0) = 0
V(s’=10/a=0) = 0.33(0+0) = 0
V(s’=14/a=0) = 0.33(0+0) = 0
V(a=0) = 0
For action 1 (i.e going down)
V(s’=14/a=1) = 0.33(0+0) = 0
V(s’=13/a=1) = 0.33(0+0) = 0
V(s’=15/a=1) = 0.33(0+1) = 0.33
V(a=1) = 0.33
For action 2 (i.e taking Right)
V(s’=15/a=2) = 0.33(0+1) = 0.33
V(s’=10/a=2) = 0.33(0+0) = 0
V(s’=14/a=2) = 0.33(0+0) = 0
V(a=2) = 0.33
For action 3 (i.e going Up)
V(s’=10/a=3) = 0.33(0+0) = 0
V(s’=13/a=3) = 0.33(0+0) = 0
V(s’=15/a=3) = 0.33(0+1) = 0.33
V(a=3) = 0.33
After first iteration the frozen lake with value of all actions look like following
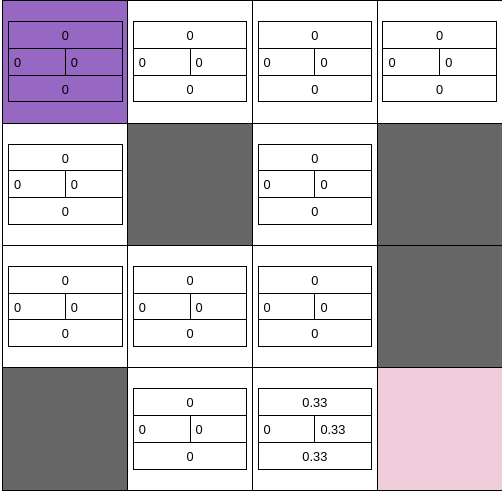
Iteration II
For state 0:
For action 0 (i.e taking Left)
V(s’=0/a=0) = 0.66(0+0) = 0
V(s’=4/a=0) = 0.33(0+0) = 0
V(a=0) = 0
For action 1 (i.e going down)
V(s’=0/a=1) = 0.33(0+0) = 0
V(s’=1/a=1) = 0.33(0+0) = 0
V(s’=4/a=1) = 0.33(0+0) = 0
V(a=1) = 0
For action 2 (i.e taking Right)
V(s’=0/a=2) = 0.33(0+0) = 0
V(s’=1/a=2) = 0.33(0+0) = 0
V(s’=4/a=2) = 0.33(0+0) = 0
V(a=2) = 0
For action 3 (i.e going Up)
V(s’=0/a=3) = 0.66(0+0) = 0
V(s’=1/a=3) = 0.33(0+0) = 0
V(a=3) = 0
In the second iteration we get value = 0 in all states for all actions except for state 14 and the states that are adjacent to it (like: 13 and 10).
For state 10:
For action 0 (i.e taking Left)
V(s’=9/a=0) = 0.33(0+0) = 0
V(s’=6/a=0) = 0.33(0+0) = 0
V(s’=14/a=0) = 0.33(0.33+0) = 0.1111
V(a=0) = 0.11
Here the highlighted value is the maximum value of the next state (i.e state 14) among possible actions.
For action 1 (i.e going down)
V(s’=14/a=1) = 0.33(0.33+0) = 0.111
V(s’=9/a=1) = 0.33(0+0) = 0
V(s’=11/a=1) = 0.33(0+0) = 0
V(a=1) = 0.11
For action 2 (i.e taking Right)
V(s’=11/a=2) = 0.33(0+0) = 0
V(s’=6/a=2) = 0.33(0+0) = 0
V(s’=14/a=2) = 0.33(0.33+0) = 0.11
V(a=2) = 0.11
For action 3 (i.e going Up)
V(s’=6/a=3) = 0.33(0+0) = 0
V(s’=9/a=3) = 0.33(0+0) = 0
V(s’=9/a=3) = 0.33(0+0) = 0
V(a=0) = 0
For state 13:
For action 0 (i.e taking Left)
V(s’=12/a=0) = 0.33(0+0) = 0
V(s’=9/a=0) = 0.33(0+0) = 0
V(s’=13/a=0) = 0.33(0+0) = 0
V(a=0) = 0
For action 1 (i.e going down)
V(s’=12/a=1) = 0.33(0+0) = 0
V(s’=13/a=1) = 0.33(0+0) = 0
V(s’=14/a=1) = 0.33(0.33+0) = 0.111
V(a=1) = 0.11
For action 2 (i.e taking Right)
V(s’=14/a=2) = 0.33(0.33+0) = 0.11
V(s’=9/a=2) = 0.33(0+0) = 0
V(s’=13/a=2) = 0.33(0+0) = 0
V(a=2) = 0.22
For action 3 (i.e going Up)
V(s’=9/a=3) = 0.33(0+0) = 0
V(s’=12/a=3) = 0.33(0+0) = 0
V(s’=14/a=3) = 0.33(0.33+0) = 0.111
V(a=3) = 0.11
For state 14:
For action 0 (i.e taking Left)
V(s’=13/a=0) = 0.33(0+0) = 0
V(s’=10/a=0) = 0.33(0+0) = 0
V(s’=14/a=0) = 0.33(0.33+0) = 0.1111
Here the highlighted value is the maximum value of the next state (i.e state 14) among possible actions.
V(a=0) = 0.11
For action 1 (i.e going down)
V(s’=14/a=1) = 0.33(0.33+0) = 0.111
V(s’=13/a=1) = 0.33(0+0) = 0
V(s’=15/a=1) = 0.33(0+1) = 0.33
V(a=1) = 0.44
For action 2 (i.e taking Right)
V(s’=15/a=2) = 0.33(1+0) = 0.33
V(s’=10/a=2) = 0.33(0+0) = 0
V(s’=14/a=2) = 0.33(0.33+0) = 0.11
V(a=2) = 0.44
For action 3 (i.e going Up)
V(s’=10/a=3) = 0.33(0+0) = 0
V(s’=13/a=3) = 0.33(0+0) = 0
V(s’=15/a=3) = 0.33(1+0) = 0.33
V(a=3) = 0.33
After second iteration the frozen lake with value of all actions look like following
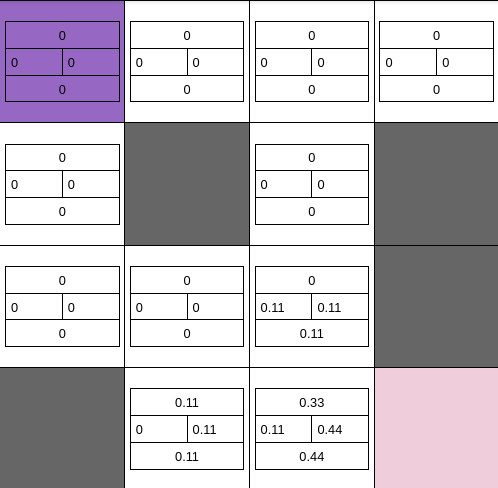
If we keep going on like this after a few hundred iterations we will get the values of all actions of all states in the following form.

If we develop our policy according to above values of actions in the given states.
Our policy for this frozen lake will look something like this.
Code for Value Iteration
size = len(P)
print(size)
#this array will keep value of all states for all actions
value_array4D = np.zeros([4,size])
for i in range(300):
#here 300 in no of iterations:
#Assuming after 300 iterations it will converge
#this array will keep value of all states for all actions for each iteration
#this array will be reset after each iteration
temp_array = np.zeros([4,size])
for j in range(len(P)-1):
#range is one less than total number of states as we are not calculating any value for last state
j= j
#print("current state",j)
#print(P[j][2])
#print(P[j][0][0][0])
if(P[j][0][0][0]!=1):
#the condition in if will exclude holes
#print(P[j][0][0][3])
sums = np.zeros(4)
for direction in range(4):
#entries is possiblie new states that an agent can reach ffrom current state by taking particular action
entries = len(P[j][direction])
#print("entries",entries)
for k in range(entries):
#print("Probability")
probability = P[j][direction][k][0]
#print(probability)
#print("next state")
next_state = P[j][direction][k][1]
#print(next_state)
#print("value of next state")
#get max value of all the action-value of next state
max_value = np.max(value_array4D[0:,next_state])
#print(max_value)
#print("max value",max_value)
#print("Reward")
#check the reward
reward = P[j][direction][k][2]
#print(reward)
#The value iteration equation
sums[direction] = sums[direction] + probability*(max_value+reward)
temp_array[direction][j] = sums[direction]
#print("sums",sums)
# print("..........\n\n")
#print(temp_array.T)
#Copy the value of temp_array in value_array4D
value_array4D = temp_array
#print("..........\n\n")
Printing value of all actions for all states
value_array4D.T
Making policy by reading the final value of value_array4D
frozen_lake = np.chararray([4,4],unicode = True)
frozen_lake_policy = np.zeros([4,4])
count = 0
for i in range(4):
for j in range(4):
if(P[count][0][0][0]!=1 and count<15):
max_value = np.argmax(value_array4D.T[count])
print(max_value)
frozen_lake_policy[i][j]=max_value
if(max_value == 0):
frozen_lake[i][j]="<"
print("<")
elif (max_value == 1):
frozen_lake[i][j]="v"
print("v")
elif (max_value == 2):
frozen_lake[i][j]=">"
print(">")
else:
frozen_lake[i][j]="^"
print("^")
elif(P[count][0][0][0]==1 and count<15):
frozen_lake[i][j] = 'H'
else:
frozen_lake[i][j] = 'End'
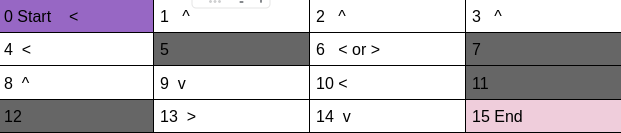
count = count+1The optimum policy of frozen Lake

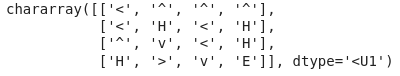
Evaluation of above policy
print(policy_testing(P,frozen_lake_policy_reshaped))This optimum policy has win rate of nearly 82%