Python
Solving Bipedal Walker Hardcore Challenge with Soft Actor-Critic Algorithm
September 27, 2024

Solving Bipedal Walker Hardcore Challenge with Soft Actor-Critic Algorithm

In this tutorial we will learn to solve Bipedal Walker Hardcore Challenge with Soft Actor-Critic Algorithm. We will start by editing the environment to favor our algorithm. This will be followed by creation of neural networks and finally we will learn to write code for Soft Actor Critic algorithm.

Creation of Custom Wrapper

This wrapper encourages the agent to be bolder by lowering failure penalties and speeds up training by skipping frames, effectively reducing the frequency at which actions are taken.

class MyWalkerWrapper(gym.Wrapper):
    '''
    This is custom wrapper for BipedalWalker-v3 and BipedalWalkerHardcore-v3.
    Rewards for failure is decreased to make agent brave for exploration and
    time frequency of dynamic is lowered by skipping two frames.
    '''
    def __init__(self, env, skip=4):
        super().__init__(env)
        self._obs_buffer = deque(maxlen=skip)
        self._skip = skip
        self._max_episode_steps = 750

    def step(self, action):
        total_reward = 0
        for i in range(self._skip):
            obs, reward, done, info = self.env.step(action)
            if self.env.game_over:
                reward = -10.0
                info["dead"] = True
            else:
            	info["dead"] = False

            self._obs_buffer.append(obs)
            total_reward += reward
            if done:
                break

        return obs, total_reward, done, info

    def reset(self):
        return self.env.reset()

    def render(self, mode="human"):
        for _ in range(self._skip):
            out = self.env.render(mode=mode)
        return out

Using the wrapper

Installation and usage

!pip install swig
!pip install gym[box2d]
import gym
print(f"Gym version: {gym.__version__}")
env = gym.make('BipedalWalker-v3', hardcore=True)
env = MyWalkerWrapper(env, skip=4)

Neural Network

We will use three neural networks.

Feed Forward Encoder

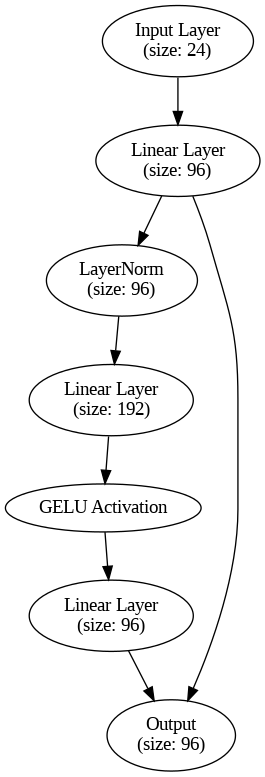
This neural network takes in data, processes it through a series of transformations, and outputs a refined version of that data. It’s structured to enhance certain features of the input, often used in tasks like natural language processing, reinforcement learning, or other machine learning applications where you need to extract complex patterns from data.

  1. Input Layer (Embedding Layer):
    • self.embedding = nn.Linear(input_size, hidden_size): This is the first transformation applied to the input. It takes the input data (of size input_size) and passes it through a linear layer, converting it into a higher-dimensional space (with size hidden_size). This is like mapping raw input data into a new representation, making it easier for the network to work with.
    • nn.init.xavier_uniform_: This function initializes the weights of the embedding layer in a specific way (Xavier initialization) to ensure that signals are properly propagated through the network, avoiding too-large or too-small gradients.
    • nn.init.zeros_: The biases (an extra adjustable parameter) in the embedding layer are set to zero to start with.
  2. FeedForward Block (self.block):
    • nn.Sequential: This is a container that applies several operations in sequence.
    • LayerNorm (nn.LayerNorm(hidden_size)): This normalizes the data by adjusting its values to have a mean of 0 and a standard deviation of 1, which helps stabilize and speed up training.
    • First Linear Layer (nn.Linear(hidden_size, ff_size)): This layer projects the data into a new space with size ff_size, expanding the number of features being processed.
    • Activation Function (GELU, nn.GELU()): The GELU activation function is applied after the first linear layer. It adds non-linearity to the model, which is important for allowing the network to learn complex patterns. GELU is smoother than more common activations like ReLU, which can improve performance in some tasks.
    • Second Linear Layer (nn.Linear(ff_size, hidden_size)): After the non-linear transformation, this layer reduces the number of features back down to the original hidden_size
  3. Forward Pass (forward method):
    • Embedding Transformation: First, the input x is passed through the embedding layer.
    • Skip Connection: Then, the block processes the transformed x. This new result is added back to the original x (called a “skip connection” or “residual connection”). This helps the network learn more effectively by preventing the original input information from being lost during transformation.
class FeedForwardEncoder(nn.Module):
    def __init__(self, input_size, hidden_size, ff_size):
        super(FeedForwardEncoder, self).__init__()
        self.embedding = nn.Linear(input_size, hidden_size)
        nn.init.xavier_uniform_(self.embedding.weight)
        nn.init.zeros_(self.embedding.bias)
        self.block = nn.Sequential(nn.LayerNorm(hidden_size), 
                                   nn.Linear(hidden_size, ff_size), nn.GELU(),
                                   nn.Linear(ff_size, hidden_size))

    def forward(self, x):
        x = self.embedding(x)
        x = x + self.block(x)
        return x

Weight Initialization: Proper weight initialization ensures that the neural network learns effectively without suffering from issues like vanishing or exploding gradients.

Layer Normalization: Helps maintain consistent activation values, making training faster and more stable.

FeedForward Block: This block is a standard building unit in many modern architectures (like Transformers), which allows the network to learn complex transformations on the data.

Skip Connection: Improves learning by passing along the original data, helping prevent information loss or degradation through the layers.

Critic Network

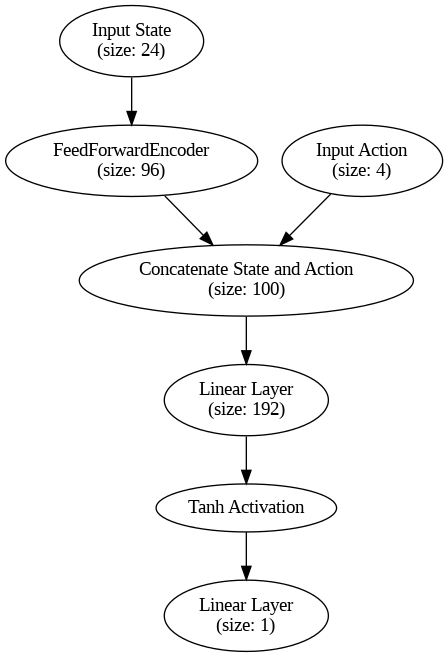
The Critic network estimates the Q-value for a state-action pair. In reinforcement learning, this value is crucial for evaluating how good a certain action is in a particular state, helping the agent learn better policies (how to act optimally).

  1. Input Parameters:
    • state_dim=24: This refers to the size of the state space, meaning the number of features that describe the current state of the environment.
    • action_dim=4: This refers to the size of the action space, i.e., the number of features that describe the action the agent is taking.
  2. State Encoder (self.state_encoder):
    • This is where the state gets transformed into a more useful representation. It uses a FeedForwardEncoder (defined in your previous example).
    • FeedForwardEncoder(self.state_dim, 96, 192): It takes the state as input (size 24), transforms it into a hidden representation of size 96, and passes it through another feedforward layer to extract features.
    • Encoding the state makes it easier for the critic to analyze and combine it with the action later.
  3. Second Layer (self.fc2):
    • Input: This layer takes the concatenated output of the state encoder (96 units) and the action (4 units). So, the input size to this layer is 96+4=100.
    • Output: The layer then produces a hidden feature vector of size 192.
    • Activation Function (Tanh): After passing through the layer, the output is passed through a Tanh activation function. This adds non-linearity, allowing the model to learn complex relationships between states and actions.
    • xavier_uniform_ ensures that the weights of this layer are initialized in a balanced way, using a gain value suitable for Tanh activation. This helps to stabilize the learning process.
  4. Output Layer (self.fc_out):
    • Linear Layer (self.fc_out): This produces a single scalar output (the estimated Q-value). The absence of a bias term means there’s no extra parameter added to this output.
    • Weight Initialization: The weights are initialized with small random values between -0.003 and +0.003. This ensures the initial predictions are close to zero, preventing extreme Q-value predictions in the beginning of training.
  5. Forward Method (forward):
    • This function defines the forward pass, which calculates the Q-value for a given state and action.
    • State Encoding: The state is passed through self.state_encoder, transforming it into a more useful feature representation s.
    • Concatenation: The encoded state (s) is concatenated with the action (action) along the last dimension (dim=1).
    • Hidden Transformation: The combined state-action vector is passed through fc2, followed by the Tanh activation function.
    • Q-Value Output: Finally, the output is scaled by 10, producing the Q-value for the given state-action pair.
class Critic(nn.Module):

    def __init__(self, state_dim=24, action_dim=4):
        """
        :param state_dim: Dimension of input state (int)
        :param action_dim: Dimension of input action (int)
        :return:
        """
        super(Critic, self).__init__()

        self.state_dim = state_dim
        self.action_dim = action_dim

        self.state_encoder = FeedForwardEncoder(self.state_dim, 96, 192)

        self.fc2 = nn.Linear(96 + self.action_dim, 192)
        nn.init.xavier_uniform_(self.fc2.weight, gain=nn.init.calculate_gain('tanh'))

        self.fc_out = nn.Linear(192, 1, bias=False)
        nn.init.uniform_(self.fc_out.weight, -0.003,+0.003)

        self.act = nn.Tanh()

    def forward(self, state, action):
        """
        returns Value function Q(s,a) obtained from critic network
        :param state: Input state (Torch Variable : [n,state_dim] )
        :param action: Input Action (Torch Variable : [n,action_dim] )
        :return: Value function : Q(S,a) (Torch Variable : [n,1] )
        """
        s = self.state_encoder(state)
        x = torch.cat((s,action),dim=1)
        x = self.act(self.fc2(x))
        x = self.fc_out(x)*10
        return x

Actor Network

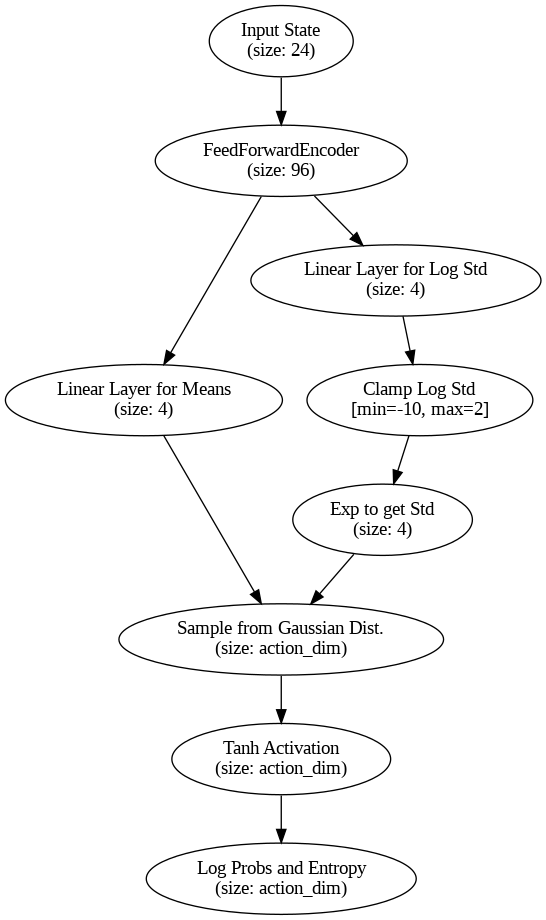
The Actor network takes a state as input and produces actions that the agent should take. It can either output a deterministic action (best guess) or a stochastic action (sampled from a probability distribution) to encourage exploration. The actions are scaled to lie within a specific range using the Tanh function, and when in stochastic mode, the model also returns entropy for exploration purposes.

  1. Input Parameters:
    • state_dim=24: The number of features representing the current state of the environment.
    • action_dim=4: The number of possible actions the agent can take.
    • stochastic=False: Controls whether the actor outputs deterministic or stochastic actions.
  2. State Encoder (self.state_encoder):
    • This transforms the input state into a more useful hidden representation.
    • FeedForwardEncoder(self.state_dim, 96, 192): The state goes through this encoder, which is designed to extract meaningful features from the state input before the action is computed.
  3. Action Layer (self.fc):
    • self.fc: This is the layer that maps the hidden state representation to the action space. It outputs the mean value of the actions if the policy is deterministic.
    • Weight Initialization: The weights are initialized with small random values between -0.003 and +0.003, ensuring that initial action predictions are close to zero.
  4. Stochastic Layer (Optional):
    • If self.stochastic=True, the network can output actions sampled from a probability distribution rather than a fixed deterministic action.
    • self.log_std: This layer outputs the logarithm of the standard deviation for each action dimension. This is part of the stochastic process for sampling actions.
    • Clamping: The standard deviations (log_stds) are clamped between -10.0 and 2.0 to prevent extreme values, ensuring reasonable variance in the action distribution.
    • Normal(means, stds): A Gaussian distribution is created with the means (from the action layer) and the standard deviations (from the log_std layer). The model then samples actions from this distribution.
  5. Activation Function (Tanh):
    • The actions are passed through a Tanh function, which squashes the output to lie within the range (-1, 1). This is important for controlling the action space within certain limits.
  6. Forward Method (forward):
    • If stochastic=True:
      • The model first calculates the mean (means) and log standard deviation (log_stds) of the action distribution.
      • It then samples an action (x) from the Gaussian distribution (using dists.rsample()) if explore=True (to allow for exploration in training). Otherwise, it directly uses the mean action.
      • The sampled action is passed through Tanh, constraining the action range to (-1, 1).
      • Additionally, the log probability of the sampled action is calculated to measure how likely the action was under the current policy. The entropy (a measure of uncertainty in the action distribution) is also computed, which is useful for encouraging exploration.
    • If stochastic=False:
      • The model outputs deterministic actions by applying Tanh to the action layer’s output (self.fc(s)), which directly produces actions in (-1, 1).

Stochastic Behavior: By having both deterministic and stochastic modes, this actor network can adapt to different exploration strategies. In stochastic mode, it samples actions from a probability distribution, encouraging exploration in early training stages. In deterministic mode, it selects the action that is most likely to be optimal.

Entropy Regularization: The inclusion of entropy helps the model maintain some level of exploration, even when the policy becomes more confident. This is crucial for algorithms like Soft Actor-Critic (SAC), which balance exploration and exploitation using entropy.

class Actor(nn.Module):

    def __init__(self, state_dim=24, action_dim=4, stochastic=False):
        """
        :param state_dim: Dimension of input state (int)
        :param action_dim: Dimension of output action (int)
        :param action_lim: Used to limit action in [-action_lim,action_lim]
        :return:
        """
        super(Actor, self).__init__()

        self.state_dim = state_dim
        self.action_dim = action_dim
        self.stochastic = stochastic

        self.state_encoder = FeedForwardEncoder(self.state_dim, 96, 192)

        self.fc = nn.Linear(96, action_dim, bias=False)
        nn.init.uniform_(self.fc.weight, -0.003,+0.003)
        #nn.init.zeros_(self.fc.bias)

        if self.stochastic:
            self.log_std = nn.Linear(96, action_dim, bias=False)
            nn.init.uniform_(self.log_std.weight, -0.003,+0.003)
            #nn.init.zeros_(self.log_std.bias)

        self.tanh = nn.Tanh()


    def forward(self, state, explore=True):
        """
        returns either:
        - deterministic policy function mu(s) as policy action.
        - stochastic action sampled from tanh-gaussian policy, with its entropy value.
        this function returns actions lying in (-1,1)
        :param state: Input state (Torch Variable : [n,state_dim] )
        :return: Output action (Torch Variable: [n,action_dim] )
        """
        s = self.state_encoder(state)
        if self.stochastic:
            means = self.fc(s)
            log_stds = self.log_std(s)
            log_stds = torch.clamp(log_stds, min=-10.0, max=2.0)
            stds = log_stds.exp()
            #print(stds)
            dists = Normal(means, stds)
            if explore:
                x = dists.rsample()
            else:
                x = means
            actions = self.tanh(x)
            log_probs = dists.log_prob(x) - torch.log(1-actions.pow(2) + 1e-6)
            entropies = -log_probs.sum(dim=1, keepdim=True)
            return actions, entropies

        else:
            actions = self.tanh(self.fc(s))
            return actions

Soft Actor Critic

The basic flow of the Soft Actor Critic algorithm.

1. Initialize actor and critic networks
   ├── Initialize Actor Network (policy) π(·|s) with random weights.
   ├── Initialize two Critic Networks Q₁(s, a) and Q₂(s, a) with random weights.
   ├── Initialize two Target Critic Networks Q₁_target and Q₂_target (copy weights from Critic networks).
   ├── Initialize Replay Buffer to store experiences.
   │
2. For each episode:
   ├── Reset the environment and get the initial state.
   │
   ├── For each timestep (t) in the episode:
   │    ├── Sample an action aₜ from the current policy π(aₜ|sₜ).
   │    │
   │    ├── Execute action aₜ in the environment, observe reward rₜ, and next state sₜ₊₁.
   │    │
   │    ├── Store experience tuple (sₜ, aₜ, rₜ, sₜ₊₁, done) in the replay buffer.
   │    │
   │    ├── If enough experiences are collected in the replay buffer:
   │    │    └── Sample a mini-batch of experiences from the replay buffer.
   │    │
   │    └── Perform **Learning Step**:
   │         ├── **Step 1: Update Critic Networks (Q₁ and Q₂)**
   │         │    ├── Sample actions from the actor for the next state sₜ₊₁.
   │         │    ├── Compute the target Q-value:
   │         │    │    └── Q_target = rₜ + γ * min(Q₁_target(sₜ₊₁, aₜ₊₁), Q₂_target(sₜ₊₁, aₜ₊₁)) + α * entropy(aₜ₊₁)
   │         │    ├── Update Q₁ and Q₂ by minimizing the MSE loss between predicted Q-values and target Q-value.
   │         │
   │         ├── **Step 2: Update the Actor Network (π)**
   │         │    ├── Sample actions from the actor for the current state sₜ.
   │         │    ├── Compute Q-values for the current state-action pair using Q₁ and Q₂.
   │         │    ├── Compute the actor loss: 
   │         │    │    └── actor_loss = -[ min(Q₁(sₜ, aₜ), Q₂(sₜ, aₜ)) + α * entropy(aₜ) ]
   │         │    ├── Perform gradient descent to update the actor (policy) network.
   │         │
   │         └── **Step 3: Soft Update Target Critic Networks**
   │              ├── Perform a soft update on Q₁_target and Q₂_target:
   │              │    └── Q_target = τ * Q_train + (1 - τ) * Q_target
   │              └── This ensures smooth updates and stability during training.
   │
   └── If the episode ends (done == True), reset the environment for the next episode.
   │
3. Save checkpoints of the trained model periodically (optional).

4. Repeat training until convergence or the desired number of episodes is reached.
  1. Initialize Actor and Critic Networks:
    • Actor (Policy) Network (π): This network outputs the action distribution given a state. It will learn a stochastic policy that maximizes expected rewards and entropy.
    • Critic Networks (Q₁, Q₂): Two Q-value networks are used to estimate the expected return (value) for a state-action pair. The dual critic architecture helps mitigate overestimation of Q-values (Double Q-learning).
    • Target Critic Networks (Q₁_target, Q₂_target): These networks are soft copies of the main critic networks and are used for computing stable Q-targets during training.
  2. Main Training Loop:
    • For each episode, reset the environment and observe the initial state. This begins a new episode where the agent interacts with the environment.
  3. Timestep Loop within Each Episode:
    • Sample Action (aₜ): The agent samples an action from the current policy π(a|sₜ) and interacts with the environment.
    • Observe Reward (rₜ) and Next State (sₜ₊₁): After executing the action, the agent observes the reward and next state returned by the environment.
    • Store Experience: The agent stores the tuple (sₜ, aₜ, rₜ, sₜ₊₁, done) in the replay buffer for future learning.
  4. Perform Learning Step (if sufficient experiences in buffer):
    • Step 1: Update Critic Networks (Q₁ and Q₂):
      • Compute Target Q-Value: The target Q-value is calculated using the reward, the next state Q-values from the target critics, and the entropy of the action predicted by the actor. The minimum of the two critic outputs is taken to avoid overestimation.
      • Update Q₁ and Q₂: Both critics are updated by minimizing the mean squared error (MSE) between the current Q-values and the target Q-values.
    • Step 2: Update the Actor Network (π):
      • Sample Actions: The actor samples an action for the current state.
      • Compute Actor Loss: The actor loss is computed as the negative expected Q-value (minimum of Q₁ and Q₂) plus an entropy regularization term. This encourages the policy to maximize the expected return while maintaining exploration through the entropy term.
      • Update Actor: The actor is updated by performing gradient descent on the actor loss.
    • Step 3: Soft Update Target Critic Networks:
      • Soft Update: The target networks (Q₁_target and Q₂_target) are updated by blending a fraction of the current critic networks with the target networks. This is done using the soft update formula:
        Q_target = τ * Q_train + (1 - τ) * Q_target.
        Soft updates help stabilize the learning process and ensure the target Q-values change smoothly over time.
  5. nd of Episode:
    • When the episode ends, the environment is reset and a new episode begins. The learning process continues until the maximum number of episodes is reached or the policy converges.
import torch
from torch import optim
import numpy as np
import os

from itertools import chain

class SACAgent():
    rl_type = 'sac'
    def __init__(self, Actor, Critic, clip_low, clip_high, state_size=24, action_size=4, update_freq=int(1),
            lr=4e-4, weight_decay=1e-3, gamma=0.98, alpha=0.01, tau=0.01, batch_size=128, buffer_size=int(500000), device=None):

        self.state_size = state_size
        self.action_size = action_size
        self.update_freq = update_freq

        self.learn_call = int(0)

        self.alpha = alpha
        self.gamma = gamma
        self.tau = tau
        self.batch_size = batch_size

        if device is None:
            self.device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
        else:
            self.device = torch.device(device)

        self.clip_low = torch.tensor(clip_low)
        self.clip_high = torch.tensor(clip_high)

        self.train_actor = Actor(stochastic=True).to(self.device)
        self.actor_optim = torch.optim.AdamW(self.train_actor.parameters(), lr=lr, weight_decay=weight_decay, amsgrad=True)
        print(f'Number of paramters of Actor Net: {sum(p.numel() for p in self.train_actor.parameters())}')

        self.train_critic_1 = Critic().to(self.device)
        self.target_critic_1 = Critic().to(self.device).eval()
        self.hard_update(self.train_critic_1, self.target_critic_1) # hard update at the beginning
        self.critic_1_optim = torch.optim.AdamW(self.train_critic_1.parameters(), lr=lr, weight_decay=weight_decay, amsgrad=True)

        self.train_critic_2 = Critic().to(self.device)
        self.target_critic_2 = Critic().to(self.device).eval()
        self.hard_update(self.train_critic_2, self.target_critic_2) # hard update at the beginning
        self.critic_2_optim = torch.optim.AdamW(self.train_critic_2.parameters(), lr=lr, weight_decay=weight_decay, amsgrad=True)
        print(f'Number of paramters of Single Critic Net: {sum(p.numel() for p in self.train_critic_2.parameters())}')

        self.memory= ReplayBuffer(action_size= action_size, buffer_size= buffer_size, \
            batch_size= self.batch_size, device=self.device)

        self.mse_loss = torch.nn.MSELoss()

    def learn_with_batches(self, state, action, reward, next_state, done):
        self.memory.add(state, action, reward, next_state, done)
        self.learn_one_step()

    def learn_one_step(self):
        if(len(self.memory)>self.batch_size):
            exp=self.memory.sample()
            self.learn(exp)

    def learn(self, exp):
        self.learn_call+=1
        states, actions, rewards, next_states, done = exp

        #update critic
        with torch.no_grad():
            next_actions, next_entropies = self.train_actor(next_states)
            Q_targets_next_1 = self.target_critic_1(next_states, next_actions)
            Q_targets_next_2 = self.target_critic_2(next_states, next_actions)
            Q_targets_next = torch.min(Q_targets_next_1, Q_targets_next_2) + self.alpha * next_entropies
            Q_targets = rewards + (self.gamma * Q_targets_next * (1-done))
            #Q_targets = rewards + (self.gamma * Q_targets_next)

        Q_expected_1 = self.train_critic_1(states, actions)
        critic_1_loss = self.mse_loss(Q_expected_1, Q_targets)
        #critic_1_loss = torch.nn.SmoothL1Loss()(Q_expected_1, Q_targets)

        self.critic_1_optim.zero_grad(set_to_none=True)
        critic_1_loss.backward()
        #torch.nn.utils.clip_grad_norm_(self.train_critic_1.parameters(), 1)
        self.critic_1_optim.step()

        Q_expected_2 = self.train_critic_2(states, actions)
        critic_2_loss = self.mse_loss(Q_expected_2, Q_targets)
        #critic_2_loss = torch.nn.SmoothL1Loss()(Q_expected_2, Q_targets)

        self.critic_2_optim.zero_grad(set_to_none=True)
        critic_2_loss.backward()
        #torch.nn.utils.clip_grad_norm_(self.train_critic_2.parameters(), 1)
        self.critic_2_optim.step()

        #update actor
        actions_pred, entropies_pred = self.train_actor(states)
        Q_pi = torch.min(self.train_critic_1(states, actions_pred), self.train_critic_2(states, actions_pred))
        actor_loss = -(Q_pi + self.alpha * entropies_pred).mean()

        self.actor_optim.zero_grad(set_to_none=True)
        actor_loss.backward()
        #torch.nn.utils.clip_grad_norm_(self.train_actor.parameters(), 1)
        self.actor_optim.step()

        if self.learn_call % self.update_freq == 0:
            self.learn_call = 0
            #using soft upates
            self.soft_update(self.train_critic_1, self.target_critic_1)
            self.soft_update(self.train_critic_2, self.target_critic_2)

    @torch.no_grad()
    def get_action(self, state, explore=True):
        #self.train_actor.eval()
        state = torch.from_numpy(state).unsqueeze(0).float().to(self.device)
        #with torch.no_grad():
        action, entropy = self.train_actor(state, explore=explore)
        action = action.cpu().data.numpy()[0]
        #self.train_actor.train()
        return action

    def soft_update(self, local_model, target_model):
        for target_param, local_param in zip(target_model.parameters(), local_model.parameters()):
            target_param.data.copy_(self.tau*local_param.data + (1.0-self.tau)*target_param.data)

    def hard_update(self, local_model, target_model):
        for target_param, local_param in zip(target_model.parameters(), local_model.parameters()):
            target_param.data.copy_(local_param.data)




    def save_ckpt(self,save_path="models/sac/sac_bipedal_redefined2.pt"):
        save_path = save_path
        # Create a dictionary containing the state_dict of the actor, critic_1, and critic_2
        checkpoint = {
            'actor': self.train_actor.state_dict(),
            'critic_1': self.train_critic_1.state_dict(),
            'critic_2': self.train_critic_2.state_dict()
        }

        # Save the dictionary to a single file
        torch.save(checkpoint, save_path)

    def load_ckpt(self,load_path="models/sac/sac_bipedal_redefined2.pt"):
        load_path = load_path

        # Load the checkpoint dictionary
        try:
            checkpoint = torch.load(load_path)

            # Load the state_dicts into the models
            self.train_actor.load_state_dict(checkpoint['actor'])
            self.train_critic_1.load_state_dict(checkpoint['critic_1'])
            self.train_critic_2.load_state_dict(checkpoint['critic_2'])
            print(f"Model loaded successfully: {load_path}")
        except:
            print("Failed to load")



    def train_bipedal_walker(self, env, num_episodes=500, max_timesteps=2000, render=False):
      """
      Trains a Soft Actor-Critic agent on the Bipedal Walker environment.

      :param agent: SACAgent object
      :param env: Bipedal Walker environment (gym.make('BipedalWalker-v3'))
      :param num_episodes: Number of episodes to train for
      :param max_timesteps: Maximum number of timesteps per episode
      :param render: Whether to render the environment or not
      """
      rewards_history = []
      for episode in range(1, num_episodes + 1):
          state = env.reset()
          episode_reward = 0

          for t in range(max_timesteps):
              if render:
                  env.render()

              # Get action from the agent
              action = self.get_action(state, explore=True)

              # Take the action in the environment
              next_state, reward, done, _ = env.step(action)

              # Clip reward to avoid large fluctuations
              reward = np.clip(reward, -10, 10)

              # Store the experience in replay buffer
              self.learn_with_batches(state, action, reward, next_state, done)

              # Move to the next state
              state = next_state
              episode_reward += reward

              if done:
                  break

          rewards_history.append(episode_reward)
          avg_reward = np.mean(rewards_history[-100:])

          print(f"Episode {episode}/{num_episodes}, Reward: {episode_reward:.2f}, Avg Reward (Last 100): {avg_reward:.2f}")

          if episode % 5 == 0:
              self.save_ckpt()

      env.close()
      return rewards_history

Output

Github Link to Code

pontu
0
Tags :

Categories

Recent Posts