Policy Gradient Implementation Using PyTorch

The policy gradient algorithm is popular method in reinforcement learning (RL) for training agents to make decisions by directly optimizing the policy, which is a function that maps states to actions.

Unlike value-based methods (like Q-learning), which learn a value function derive the policy, policy gradient methods learn the policy directly. Here is a general overview of how the policy gradient algorithm.

Key Concepts

Policy (π): A policy π(a|s; θ) is a probability distribution over actions given a state, parameterized by θ. The goal is to find the optimal policy parameters θ* that maximize the expected cumulative reward.

Reward (R): The reward is a scalar feedback signal received after taking an action in a particular state. The goal is to maximize the expected sum of rewards over time.

Return (G): The return G_t is the total discounted reward from time step t onwards, defined as:

where γ (0 ≤ γ < 1) is the discount factor.

Objective Function (J): The objective is to maximize the expected return from the start state:

Steps of the Policy Gradient Algorithm

Initialize the Policy:

Initialize the policy parameters θ (e.g., weights of a neural network).

Collect Trajectories:

Run the policy in the environment to collect trajectories (sequences of states, actions, and rewards).

A trajectory τ is a sequence (s₀, a₀, r₁, s₁, a₁, r₂, …)

Compute the Return:

For each trajectory, compute the return G_t for each time step t.

Compute the Policy Gradient:

The policy gradient is the gradient of the expected return with respect to the policy parameters θ. It can be estimated using the log-likelihood trick:

In practice, this expectation is approximated by averaging over the collected trajectories:

​

where N is the number of trajectories and T is the length of each trajectory.

∇θ​J(θ) represents the gradient of the expected return J(θ) with respect to the policy parameters θ.

N is the number of episodes.

T is the length of each episode.

∇θ​logπ(aⁱ_t∣sⁱ_t​;θ) is the gradient of the log-probability of taking action aⁱ_t given state sⁱ_t​ and policy parameters θ.

Gⁱ_t is the return (cumulative discounted reward) starting from time step t in episode i.

This formula is used to update the policy parameters θ in policy gradient methods by estimating the gradient of the expected return with respect to the policy parameters. The term Gⁱ_t acts as a weight for the gradient, indicating how favorable the taken actions were based on the observed returns. The average over N episodes ensures that the gradient estimate is based on multiple trajectories, providing a more robust estimate.

Update the Policy:

Update the policy parameters using gradient ascent: where α is the learning rate.

Repeat:

Repeat the process of collecting trajectories, computing returns, estimating the policy gradient, and updating the policy until convergence or for a fixed number of iterations.

Implementation in PyTorch

Import

import gym
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
from collections import deque
import random

Create a Class of PolicyNetwork

class PolicyNetwork(nn.Module):
    def __init__(self, state_dim, action_dim, hidden_dim=256):
        super(PolicyNetwork, self).__init__()
        self.fc1 = nn.Linear(state_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, hidden_dim)
        self.fc3 = nn.Linear(hidden_dim, action_dim)
        self.relu = nn.ReLU()

    def forward(self, x, temperature=1.0):
        x = self.relu(self.fc1(x))
        x = self.relu(self.fc2(x))
        x = self.fc3(x)
        return nn.Softmax(dim=-1)(x / temperature)

The PolicyNetwork class defines a neural network with two hidden layers and an output layer that produces a probability distribution over actions. It is commonly used in reinforcement learning tasks where the policy (the strategy of choosing actions) needs to be learned. The ReLU activation functions add non-linearity, and the softmax function ensures that the output is a valid probability distribution, which can be influenced by the temperature parameter to adjust the exploration-exploitation balance.

PolicyGradientAgent

The PolicyGradientAgent class encapsulates a typical workflow for an RL agent using policy gradient methods, focusing on policy optimization through direct gradient ascent on the expected reward.

class PolicyGradientAgent:
    def __init__(self, state_dim, action_dim, hidden_dim=256, lr=0.001, gamma=0.99, temperature=1.0):
        self.policy_net = PolicyNetwork(state_dim, action_dim, hidden_dim)
        self.optimizer = optim.Adam(self.policy_net.parameters(), lr=lr)
        self.gamma = gamma
        self.temperature = temperature
        self.memory = []

    def choose_action(self, state):
        state = torch.FloatTensor(state).unsqueeze(0)
        probs = self.policy_net(state, self.temperature).detach().numpy()[0]
        action = np.random.choice(len(probs), p=probs)
        return action

    def store_transition(self, transition):
        self.memory.append(transition)

    def learn(self):
        states, actions, rewards = zip(*self.memory)

        rewards = normalize_rewards(rewards)  # Normalize rewards

        G = np.zeros_like(rewards, dtype=np.float64)
        for t in range(len(rewards)):
            G_sum = 0
            discount = 1
            for k in range(t, len(rewards)):
                G_sum += rewards[k] * discount
                discount *= self.gamma
            G[t] = G_sum

        G = torch.FloatTensor(G)
        states = torch.FloatTensor(states)
        actions = torch.LongTensor(actions)

        self.optimizer.zero_grad()
        loss = 0
        for i in range(len(G)):
            state = states[i]
            action = actions[i]
            Gt = G[i]

            probs = self.policy_net(state)
            log_prob = torch.log(probs[action])
            entropy = -torch.sum(probs * torch.log(probs))
            loss += -log_prob * Gt - 0.01 * entropy  # Entropy regularization

        loss.backward()
        self.optimizer.step()
        self.memory = []

    def save_model(self, path):
        torch.save({
            'model_state_dict': self.policy_net.state_dict(),
            'optimizer_state_dict': self.optimizer.state_dict()
        }, path)

    def load_model(self, path, device):
        checkpoint = torch.load(path, map_location=device)
        self.policy_net.load_state_dict(checkpoint['model_state_dict'])
        self.optimizer.load_state_dict(checkpoint['optimizer_state_dict'])
        self.device = device
        self.policy_net.to(device)

Initialization (__init__)

• Parameters:
  • state_dim: Dimensionality of the state space.
  • action_dim: Dimensionality of the action space.
  • hidden_dim: Size of the hidden layer in the neural network (default: 256).
  • lr: Learning rate for the optimizer (default: 0.001).
  • gamma: Discount factor for future rewards (default: 0.99).
  • temperature: Temperature parameter for action selection, controlling exploration (default: 1.0).
• Attributes:
  • policy_net: Instance of PolicyNetwork, the neural network used to approximate the policy.
  • optimizer: Adam optimizer for updating the network’s weights.
  • gamma: Discount factor for computing the return.
  • temperature: Temperature for scaling action probabilities.
  • memory: List to store transitions ((state, action, reward)).

Methods

• choose_action(state):
  • Takes the current state as input and returns an action based on the policy network’s output probabilities.
  • Uses the temperature parameter to adjust the action probabilities and samples an action accordingly.
• store_transition(transition):
  • Stores a transition tuple (state, action, reward) in the agent’s memory for later use in training.
• learn():
  • Trains the policy network using the stored transitions.
  • Steps:
    1. Extracts and normalizes rewards.
    2. Computes the discounted return (G) for each time step.
    3. Converts states, actions, and returns to PyTorch tensors.
    4. Calculates the policy loss using the log-probability of the taken actions, weighted by the returns.
    5. Includes an entropy term to encourage exploration.
    6. Performs backpropagation and updates the network parameters.
  • Clears the memory after each learning update.
• save_model(path):
  • Saves the state dictionaries of the policy network and optimizer to the specified path.
• load_model(path, device):
  • Loads the state dictionaries of the policy network and optimizer from the specified path.
  • Transfers the network to the specified device (e.g., CPU or GPU).

Normalize Rewards

The normalize_rewards function standardizes a list of rewards by converting them to have a mean of 0 and a standard deviation of 1.

def normalize_rewards(rewards):
    rewards = np.array(rewards)
    rewards = (rewards - np.mean(rewards)) / (np.std(rewards) + 1e-9)
    return rewards.tolist()

Why Normalize Rewards?

1. Stabilize Training:
   • Reinforcement learning algorithms, particularly those involving neural networks, can be sensitive to the scale of the rewards. Large variations in reward values can cause instability in the training process. Normalizing rewards helps in making the learning process more stable and efficient.
2. Speed Up Convergence:
   • By ensuring the rewards are on a consistent scale, the optimizer can work more effectively. This can result in faster convergence of the learning algorithm, as the updates to the policy network become more consistent.
3. Reduce Reward Magnitude Differences:
   • If the rewards have very different magnitudes, the learning algorithm might prioritize high-magnitude rewards and ignore smaller ones. Normalization ensures that all rewards are considered more equally, allowing the agent to learn from a wider range of experiences.

Hyperparameters and Initialization

episodes=2000
max_timesteps=1000
env = gym.make('LunarLander-v2')
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
agent = PolicyGradientAgent(state_dim, action_dim, temperature=1.0)
rewards_per_episode = []

Try to Load a learnt model and train again

save_path='policy_gradient_model_3.pth'

try:

    agent.load_model(save_path, device='cpu')
    print("Loading successful")

except FileNotFoundError:
    print("No checkpoint found, starting from scratch.")

Train

The following code trains a reinforcement learning agent using the policy gradient method over a specified number of episodes. In each episode, the agent interacts with the environment, stores transitions, and learns from them. Rewards per episode are tracked, and the model is periodically saved. If the average reward over the last five episodes reaches a threshold, training stops, indicating convergence.

Initialization and Episode Loop

for episode in range(episodes):
    state = env.reset()
    total_reward = 0

Purpose: Loop over a specified number of episodes.

Details: Reset the environment to get the initial state and initialize the total reward for the current episode.

Timestep Loop and Action Selection

    for t in range(max_timesteps):
        action = agent.choose_action(state)
        next_state, reward, done, _ = env.step(action)
        agent.store_transition((state, action, reward))
        state = next_state
        total_reward += reward
        if done:
            break

Purpose: Loop over timesteps within an episode.

Details:

• Select an action based on the current state.
• Take a step in the environment using the chosen action.
• Store the transition (state, action, reward).
• Update the current state and accumulate the reward.
• Exit the loop if the episode is done.

Learning and Reward Tracking

    agent.learn()
    rewards_per_episode.append(total_reward)

Purpose: Update the agent’s policy and track the episode’s total reward.Details:

• Perform a learning step based on the stored transitions.
• Append the total reward of the current episode to the rewards list.

Logging and Model Saving

    print(f'Episode {episode + 1}, Reward: {total_reward}')
    if (episode + 1) % 5 == 0:
        agent.save_model(save_path)

        avg_reward = np.mean(rewards_per_episode[-5:])

        if avg_reward >= 200:  # Convergence criteria for Lunar Lander
            agent.save_model(save_path)
            print("Converged!")
            break

Purpose: Print episode information, save the model periodically, and check for convergence.

Details:

• Print the total reward for the current episode.
• Every 5 episodes, save the model and calculate the average reward of the last 5 episodes.
• If the average reward meets the convergence criterion (e.g., 200 for Lunar Lander), save the model again, print a convergence message, and terminate the training loop.

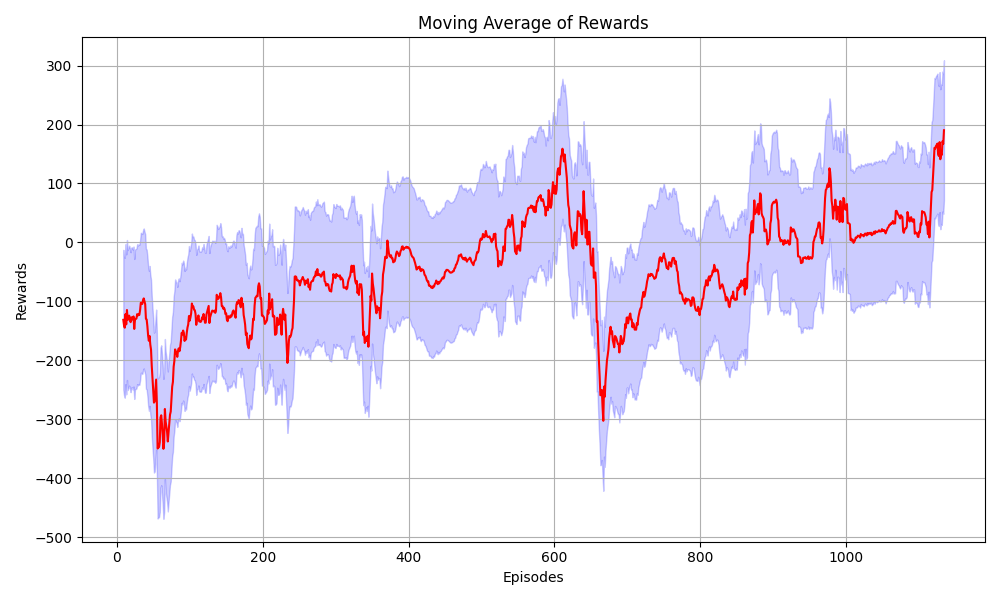
Plot the Progress

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

# Generate some sample data
np.random.seed(0)
data = rewards_per_episode

# Calculate the moving average
window_size = 10
moving_avg = pd.Series(data).rolling(window=window_size).mean()

# Plotting
plt.figure(figsize=(10, 6))

# Plot the moving average line
sns.lineplot(data=moving_avg, color='red')

# Shade the area around the moving average line to represent the range of values
plt.fill_between(range(len(moving_avg)),
                 moving_avg - np.std(data),
                 moving_avg + np.std(data),
                 color='blue', alpha=0.2)

plt.xlabel('Episodes')
plt.ylabel('Rewards')
plt.title('Moving Average of Rewards')
plt.grid(True)
# Adjust layout to prevent overlapping elements
plt.tight_layout()

# Save the plot as a PNG file
plt.savefig('Episode_rewards.png')
# Show the plot
plt.show()

Github Link