Building NanoGPT from Scratch in PyTorch: A Beginner-Friendly Guide to Transformers

In this tutorial, we will walk through the process of building NanoGPT step by step using PyTorch. You’ll start by preparing the dataset, encoding text into tokens, and creating embeddings. Then, we’ll dive into the core components of a transformer: self-attention, multi-head attention, feedforward layers, and transformer blocks. Along the way, you’ll learn how each part contributes to making GPT work. Finally, you’ll train NanoGPT on a small dataset—in this case, the poetry of John Keats—and use it to generate new text. By the end, you’ll not only have a working implementation of NanoGPT but also a solid understanding of how GPT models are built from the ground up.

Table of contents

• Import
• Data Preparation
• Get a Batch of Data
• Calculating Loss
• Self Attention
• Multihead
• Feed Forward Network
• Transformer Block
• Bigram Model
• Hpyerparameters
• Training
• Output
• Links

Import

import torch
import torch.nn as nn
from torch.nn import functional as F

This code snippet imports PyTorch, a popular deep learning framework, along with its neural network module (torch.nn) and the functional API (torch.nn.functional as F). PyTorch provides the building blocks for creating and training deep learning models: torch handles tensors and GPU acceleration, nn contains pre-built layers and model components like linear layers, embeddings, and convolutions, while functional gives you access to operations such as activation functions, loss functions, and other utilities that don’t require maintaining parameters. Together, these three imports form the essential toolkit for defining, training, and running neural networks in PyTorch.

Data Preparation

with open('/content/drive/MyDrive/Colab Notebooks/GPT/keats.txt', 'r', encoding='utf-8') as f:
    text = f.read()

This line of code opens the file keats.txt (stored in your Google Drive under Colab Notebooks/GPT) in read mode with UTF-8 encoding to properly handle text characters. Using the with open(...) as f: syntax ensures that the file is automatically closed after reading, which is a good Python practice. The f.read() function then loads the entire content of the file into the variable text as a single string. In this case, it means all of John Keats’ poetry from the text file is now available in memory for further processing, such as tokenization and training the NanoGPT model.

chars = sorted(list(set(text)))

This line extracts all the unique characters from the text and sorts them into a list. First, set(text) creates a collection of distinct characters that appear in the dataset, ensuring no duplicates. Then, list(set(text)) converts that set into a list, and finally, sorted(...) arranges the characters in a consistent, alphabetical order. The result, stored in chars, is the complete vocabulary of symbols—letters, punctuation marks, spaces, and line breaks—that the NanoGPT model will learn from and use to generate new text.

vocab_size = len(chars)

This counts how many unique characters exist in the dataset, which becomes the size of the vocabulary.

stoi = { ch:i for i,ch in enumerate(chars) }

stoi (string-to-integer) is a dictionary that maps each character ch to a unique integer i, created using enumerate(chars)

itos = { i:ch for i,ch in enumerate(chars) }

itos (integer-to-string) does the opposite, mapping each integer index back to its corresponding character.

Together, these mappings allow the text to be encoded into numbers for the model to process and then decoded back into text when generating output.

encode = lambda s: [stoi[c] for c in s] # encoder: take a string, output a list of integers
decode = lambda l: ''.join([itos[i] for i in l]) # decoder: take a list of integers, output a string

These two lines define helper functions for converting between text and numbers. The encode function takes a string s and uses the stoi dictionary to turn each character into its corresponding integer, producing a list of token IDs. For example, "cat" might become [5, 12, 20]. The decode function does the reverse: it takes a list of integers l and uses the itos dictionary to map each number back to a character, then joins them into a single string. Together, these functions let you seamlessly move between human-readable text and the numerical representation required by the NanoGPT model.

# Train and test splits
data = torch.tensor(encode(text), dtype=torch.long)
n = int(0.9*len(data)) # first 90% will be train, rest val
train_data = data[:n]
val_data = data[n:]

This block prepares the dataset for training and evaluation. First, the entire text is converted into a sequence of integers using encode(text) and wrapped in a PyTorch tensor with type torch.long, which is the standard data type for token IDs. Then, the dataset is split into two parts: 90% for training and 10% for validation. The variable n marks the split point, so train_data = data[:n] contains the training portion, while val_data = data[n:] contains the validation portion. This ensures that the model learns from one subset of the data and is evaluated on a separate, unseen subset to check its generalization ability.

Get a Batch of Data

def get_batch(split):
    # generate a small batch of data of inputs x and targets y
    data = train_data if split == 'train' else val_data
    ix = torch.randint(len(data) - block_size, (batch_size,))
    x = torch.stack([data[i:i+block_size] for i in ix])
    y = torch.stack([data[i+1:i+block_size+1] for i in ix])
    x, y = x.to(device), y.to(device)
    return x, y

This function generates a mini-batch of training or validation data for the model. It works as follows: based on the split argument, it selects either the training set (train_data) or the validation set (val_data). Then, it randomly picks starting indices ix within the dataset, making sure there’s enough room to extract a full block of length block_size. For each index, it creates an input sequence x consisting of block_size tokens and a corresponding target sequence y which is simply the same sequence shifted by one position (so the model learns to predict the next character). The inputs and targets are stacked into tensors of shape (batch_size, block_size), moved onto the correct device (CPU or GPU), and returned. In short, get_batch prepares the small chunks of text the model will train on.

Calculating Loss

@torch.no_grad()
def estimate_loss():
    out = {}
    model.eval()
    for split in ['train', 'val']:
        losses = torch.zeros(eval_iters)
        for k in range(eval_iters):
            X, Y = get_batch(split)
            logits, loss = model(X, Y)
            losses[k] = loss.item()
        out[split] = losses.mean()
    model.train()
    return out

This function is used to evaluate the model’s performance on both the training and validation sets without updating the weights.

The decorator @torch.no_grad() tells PyTorch not to track gradients, which saves memory and speeds things up since no backpropagation is needed.

Inside the function, the model is first set to evaluation mode with model.eval(), which disables certain layers like dropout.

For each split ('train' and 'val'), it repeatedly samples batches using get_batch, runs them through the model to compute the loss, and stores the results in a tensor. After averaging the collected losses, the mean loss for each split is saved in the dictionary out.

Finally, the model is put back into training mode with model.train(). The function returns the dictionary containing the average training loss and validation loss, giving a snapshot of how well the model is learning and generalizing.

Self Attention

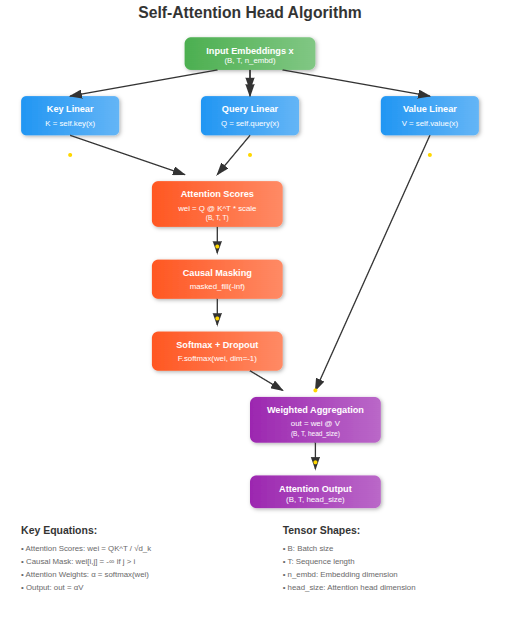
Self-attention is a mechanism in deep learning that allows a model to focus on different parts of a sequence when processing information, making it especially powerful for handling text, speech, or any sequential data.

Instead of treating each element independently, self-attention enables the model to compute relationships between elements, regardless of their distance in the sequence. The three main components of self-attention are queries (Q), keys (K), and values (V)—all learned linear transformations of the input. Intuitively, the query represents “what we are looking for,” the key encodes “what each position has to offer,” and the value carries the actual information to be aggregated.

The input to self-attention is a sequence of embeddings (e.g., word embeddings), and the output is a sequence of the same shape but enriched with contextual information, where each position attends to other positions based on learned relevance scores.

During training, the model learns the projection matrices (the weights of the linear layers generating Q, K, and V) that determine how attention scores are computed and how information flows across positions. This learning process allows the model to discover meaningful dependencies, such as which words in a sentence are most relevant to each other, ultimately enabling more accurate predictions in tasks like translation, summarization, or text generation.

class Head(nn.Module):
    """ one head of self-attention """

    def __init__(self, head_size):
        super().__init__()
        self.key = nn.Linear(n_embd, head_size, bias=False)
        self.query = nn.Linear(n_embd, head_size, bias=False)
        self.value = nn.Linear(n_embd, head_size, bias=False)
        self.register_buffer('tril', torch.tril(torch.ones(block_size, block_size)))

        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        B,T,C = x.shape
        k = self.key(x)   # (B,T,C)
        q = self.query(x) # (B,T,C)
        # compute attention scores ("affinities")
        wei = q @ k.transpose(-2,-1) * C**-0.5 # (B, T, C) @ (B, C, T) -> (B, T, T)
        wei = wei.masked_fill(self.tril[:T, :T] == 0, float('-inf')) # (B, T, T)
        wei = F.softmax(wei, dim=-1) # (B, T, T)
        wei = self.dropout(wei)
        # perform the weighted aggregation of the values
        v = self.value(x) # (B,T,C)
        out = wei @ v # (B, T, T) @ (B, T, C) -> (B, T, C)
        return out

The Head class implements a single head of self-attention, which is the core building block of the Transformer architecture.

• It takes an input sequence of embeddings (shape (B, T, C) where B=batch size, T=sequence length, C=embedding dimension).
• It projects them into queries (Q), keys (K), and values (V).
• It computes attention weights between positions using Q and K.
• Then it aggregates values (V) based on those weights.
• The output is a context-enriched sequence of the same shape (B, T, head_size).

Methods

__init__: Defines the layers and components needed for attention (linear projections for Q, K, V, causal mask, dropout).

forward: Implements the self-attention operation on input x.

Line-by-Line Code Walkthrough

class Head(nn.Module):
    """ one head of self-attention """

Defines a PyTorch module representing one attention head.

def __init__(self, head_size):
    super().__init__()
    self.key = nn.Linear(n_embd, head_size, bias=False)
    self.query = nn.Linear(n_embd, head_size, bias=False)
    self.value = nn.Linear(n_embd, head_size, bias=False)

Defines three linear layers (without bias):

• key: projects input embeddings → keys (K).
• query: projects input embeddings → queries (Q).
• value: projects input embeddings → values (V).

Each has input size n_embd (embedding dim) and output size head_size (per-head dimension).

 self.register_buffer('tril', torch.tril(torch.ones(block_size, block_size)))

• Creates a lower-triangular matrix of ones (block_size × block_size).
• Stored as a buffer (not a learnable parameter).
• Used as a causal mask: ensures each position attends only to current and past tokens, not future ones.

self.dropout = nn.Dropout(dropout)

Adds dropout for regularization, applied to attention weights.

def forward(self, x):
    B,T,C = x.shape

Extracts batch size B, sequence length T, and embedding dimension C. Input x has shape (B, T, C).

k = self.key(x)   # (B,T,C)
q = self.query(x) # (B,T,C)

Applies learned projections to get keys (k) and queries (q).

Both have shape (B, T, head_size).

# compute attention scores ("affinities")
wei = q @ k.transpose(-2,-1) * C**-0.5 

• Matrix multiplication:
  • q shape (B, T, head_size)
  • k.transpose(-2,-1) shape (B, head_size, T)
  • Result: (B, T, T) = attention scores between all token pairs.
• Scaled by 1/sqrt{C}to stabilize gradients.

wei = wei.masked_fill(self.tril[:T, :T] == 0, float('-inf'))

Applies causal mask: replaces illegal future positions with -inf, so after softmax they become 0 probability.

wei = F.softmax(wei, dim=-1) # (B, T, T)

Normalizes attention scores row-wise into probabilities.

wei = self.dropout(wei)

Randomly drops some attention links during training (regularization).

v = self.value(x) # (B,T,C)

Projects input into values (v) of shape (B, T, head_size).

out = wei @ v # (B, T, T) @ (B, T, C) -> (B, T, C)
  return out

Returns context-aware embeddings (B, T, head_size).

This class takes a sequence of embeddings, builds Q/K/V, computes scaled dot-product attention with causal masking, and outputs a new sequence enriched with contextual dependencies

Multihead

MultiHeadAttention takes a sequence of embeddings as input and applies multiple self-attention heads in parallel. Each head focuses on different types of relationships between tokens by projecting the input into different subspaces (queries, keys, values). Their outputs are concatenated and passed through a final linear layer (projection) followed by dropout. The output is a sequence of the same shape as the input, but now enriched with multiple perspectives of contextual information. The purpose is to allow the model to capture richer dependencies in the sequence than a single attention head could.

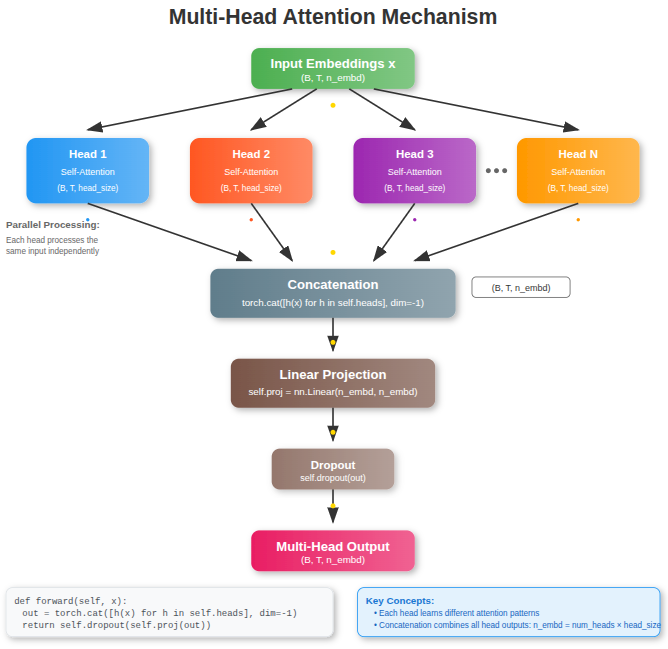
class MultiHeadAttention(nn.Module):
    """ multiple heads of self-attention in parallel """

Defines a module for multi-head attention, a key part of Transformers.

def __init__(self, num_heads, head_size):
    super().__init__()

num_heads: how many attention heads to use.

head_size: the dimensionality of each head’s output (so total output = num_heads × head_size).

self.heads = nn.ModuleList([Head(head_size) for _ in range(num_heads)])

• Creates multiple Head objects (our earlier self-attention class).
• Each head learns separate query/key/value projections.

self.proj = nn.Linear(n_embd, n_embd)

After concatenating the outputs of all heads, this linear layer projects back to the embedding dimension n_embd (to keep the dimensions consistent for later layers).

self.dropout = nn.Dropout(dropout)

Applies dropout for regularization, preventing overfitting.

def forward(self, x):
    out = torch.cat([h(x) for h in self.heads], dim=-1)

• Passes the same input x into each head.
• Each head outputs context-aware embeddings.
• Concatenates them along the embedding dimension (dim=-1).

out = self.dropout(self.proj(out))

• Applies the final projection to combine all heads’ results into one embedding space.
• Dropout adds regularization.

return out

Returns the enriched embedding sequence with the same shape as input (B, T, n_embd), but now containing multiple perspectives of attention.

Feed Forward Network

The FeedForward class is a position-wise fully connected network used in Transformers. It takes embeddings of size n_embd as input, expands them to a higher-dimensional space (4 * n_embd) to allow richer feature interactions, applies a non-linearity (ReLU) to introduce complexity, then projects back to the original embedding size. Finally, dropout is applied for regularization. This helps the model learn more powerful transformations on each token independently, complementing the contextual mixing done by self-attention.

class FeedFoward(nn.Module):
    """ a simple linear layer followed by a non-linearity """

    def __init__(self, n_embd):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(n_embd, 4 * n_embd),
            nn.ReLU(),
            nn.Linear(4 * n_embd, n_embd),
            nn.Dropout(dropout),
        )

    def forward(self, x):
        return self.net(x)

Transformer Block

The Block class represents a single Transformer block, which is the fundamental building unit of Transformer architectures.

It takes a sequence of embeddings (B, T, n_embd) as input and outputs a sequence of the same shape, but enriched with contextual and transformed information.

The block has two main components: multi-head self-attention (sa) for communication across tokens, and a feed-forward network (ffwd) for computation at each position.

Each component is preceded by layer normalization (ln1, ln2) to stabilize training, and followed by a residual connection (x + ...) to preserve the original input and improve gradient flow.

The flow is: input → normalized → self-attention → residual add, then normalized → feed-forward → residual add. Together, this structure allows the block to both mix information across tokens and transform it nonlinearly, forming the foundation for deep stacking in Transformers.

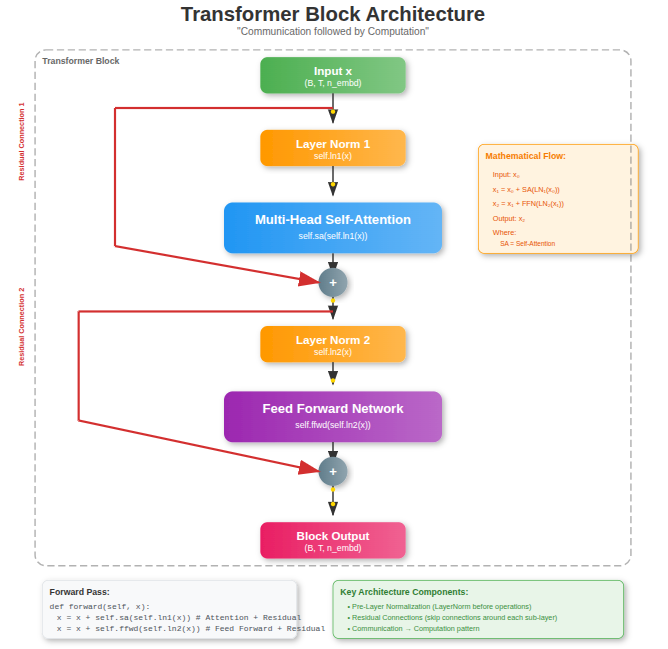
class Block(nn.Module):
    """ Transformer block: communication followed by computation """

    def __init__(self, n_embd, n_head):
        # n_embd: embedding dimension, n_head: the number of heads we'd like
        super().__init__()
        head_size = n_embd // n_head
        self.sa = MultiHeadAttention(n_head, head_size)
        self.ffwd = FeedFoward(n_embd)
        self.ln1 = nn.LayerNorm(n_embd)
        self.ln2 = nn.LayerNorm(n_embd)

    def forward(self, x):
        x = x + self.sa(self.ln1(x))
        x = x + self.ffwd(self.ln2(x))
        return x

Bigram Model

The BigramLanguageModel is a simplified Transformer-based neural network designed for next-token prediction in language modeling tasks. Its inputs are integer token indices shaped (B, T) where B is the batch size and T is the sequence length, and its outputs are logits of shape (B, T, vocab_size) that represent unnormalized probabilities of the next token.

The core components of the model include: a token embedding table that converts tokens into dense vector representations, a position embedding table that encodes sequence order, a stack of Transformer blocks (each combining multi-head self-attention and feedforward networks with layer normalization and residual connections), a final layer normalization for stability, and a linear head (lm_head) that maps embeddings back to vocabulary logits.

The purpose of the model is to learn patterns in sequences so that it can predict the most likely next token given a context.

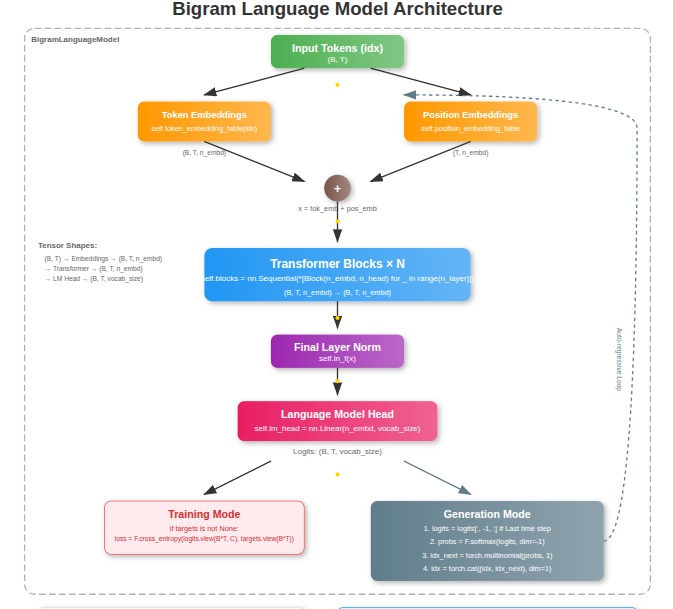
# super simple bigram model
class BigramLanguageModel(nn.Module):

    def __init__(self):
        super().__init__()
        # each token directly reads off the logits for the next token from a lookup table
        self.token_embedding_table = nn.Embedding(vocab_size, n_embd)
        self.position_embedding_table = nn.Embedding(block_size, n_embd)
        self.blocks = nn.Sequential(*[Block(n_embd, n_head=n_head) for _ in range(n_layer)])
        self.ln_f = nn.LayerNorm(n_embd) # final layer norm
        self.lm_head = nn.Linear(n_embd, vocab_size)

    def forward(self, idx, targets=None):
        B, T = idx.shape

        # idx and targets are both (B,T) tensor of integers
        tok_emb = self.token_embedding_table(idx) # (B,T,C)
        pos_emb = self.position_embedding_table(torch.arange(T, device=device)) # (T,C)
        x = tok_emb + pos_emb # (B,T,C)
        x = self.blocks(x) # (B,T,C)
        x = self.ln_f(x) # (B,T,C)
        logits = self.lm_head(x) # (B,T,vocab_size)

        if targets is None:
            loss = None
        else:
            B, T, C = logits.shape
            logits = logits.view(B*T, C)
            targets = targets.view(B*T)
            loss = F.cross_entropy(logits, targets)

        return logits, loss

    def generate(self, idx, max_new_tokens):
        # idx is (B, T) array of indices in the current context
        for _ in range(max_new_tokens):
            # crop idx to the last block_size tokens
            idx_cond = idx[:, -block_size:]
            # get the predictions
            logits, loss = self(idx_cond)
            # focus only on the last time step
            logits = logits[:, -1, :] # becomes (B, C)
            # apply softmax to get probabilities
            probs = F.softmax(logits, dim=-1) # (B, C)
            # sample from the distribution
            idx_next = torch.multinomial(probs, num_samples=1) # (B, 1)
            # append sampled index to the running sequence
            idx = torch.cat((idx, idx_next), dim=1) # (B, T+1)
        return idx

Within the class, the forward method handles embedding lookup, positional encoding, passage through Transformer blocks, and producing logits; it also computes cross-entropy loss if target tokens are provided, making the model suitable for supervised training.

The generate method is used for autoregressive text generation: given an initial context, it iteratively predicts the next token distribution, samples a token, and appends it to the sequence until the desired number of new tokens are produced.

This makes the model both a learner of sequence distributions and a generator of new text based on learned statistical dependencies.

Line-by-Line Code Walkthrough

class BigramLanguageModel(nn.Module):

Defines a PyTorch neural network module called BigramLanguageModel, inheriting from nn.Module.

def __init__(self):
    super().__init__()

Calls the parent constructor to initialize the base nn.Module.

self.token_embedding_table = nn.Embedding(vocab_size, n_embd)

• Creates an embedding table that maps each token ID (0 to vocab_size-1) to a dense vector of size n_embd.
• Purpose: turn discrete tokens into continuous representations.

self.position_embedding_table = nn.Embedding(block_size, n_embd)

• Adds a learned positional embedding for each position in the sequence (up to block_size tokens).
• Purpose: since self-attention has no inherent sense of order, this gives the model information about token positions.

self.blocks = nn.Sequential(*[Block(n_embd, n_head=n_head) for _ in range(n_layer)])

• Builds a stack of Transformer blocks (n_layer layers deep).
• Each Block has:
  • Multi-head self-attention
  • Feedforward network
  • LayerNorm + residual connections
• Purpose: let tokens “talk to each other” and build contextualized representations.

self.ln_f = nn.LayerNorm(n_embd) # final layer norm

• Applies Layer Normalization at the very end for stability.
• Purpose: helps gradients flow better, prevents exploding/vanishing.

self.lm_head = nn.Linear(n_embd, vocab_size)

• Final linear layer mapping hidden embeddings back into logits over the vocabulary.
• Purpose: converts context-aware embeddings into predictions for the next token.

def forward(self, idx, targets=None):
    B, T = idx.shape

• idx: (B, T) input tensor of token IDs.
• targets: (B, T) ground truth labels (optional, used for training).
• Extracts batch size B and sequence length T.

tok_emb = self.token_embedding_table(idx) # (B,T,C)

• Looks up embeddings for each token in the batch.
• Shape: (B, T, C) where C = n_embd.

pos_emb = self.position_embedding_table(torch.arange(T, device=device)) # (T,C)

• Creates embeddings for positions [0, 1, 2, ..., T-1].
• Shape: (T, C).

x = tok_emb + pos_emb # (B,T,C)

• Adds token and position embeddings together.
• Shape: (B, T, C) (now tokens know both identity and position).

x = self.blocks(x) # (B,T,C)

• Passes embeddings through the Transformer block stack.
• Each block applies self-attention + feedforward, refining representations.

x = self.ln_f(x) # (B,T,C)

• Applies final LayerNorm.
• Normalizes each token’s embedding for stability.

logits = self.lm_head(x) # (B,T,vocab_size)

• Projects embeddings into vocabulary space.
• Shape: (B, T, vocab_size).
• Each position has a distribution over possible next tokens.

if targets is None:
    loss = None

• If no targets given (e.g., during generation), don’t compute loss.

else:
    B, T, C = logits.shape
    logits = logits.view(B*T, C)
    targets = targets.view(B*T)
    loss = F.cross_entropy(logits, targets)

• Flattens logits and targets into (B*T, vocab_size) and (B*T,).
• Computes cross-entropy loss between predictions and ground truth.
• Purpose: train model to maximize probability of correct next token.

return logits, loss

• logits: predicted next-token scores.
• loss: training loss (or None if not provided).

def generate(self, idx, max_new_tokens):

• Autoregressive text generation method.
• Starts from an initial context idx and generates max_new_tokens.

for _ in range(max_new_tokens):
    idx_cond = idx[:, -block_size:]

• Takes only the last block_size tokens as context (since model has a fixed context window).

logits, loss = self(idx_cond)

• Runs forward pass on current context.
• Gets next-token logits.

logits = logits[:, -1, :] # becomes (B, C)

• Focus on the last position’s logits (the next-token prediction).
• Shape: (B, vocab_size).

probs = F.softmax(logits, dim=-1) # (B, C)

• Converts logits into probabilities with softmax.
• Shape: (B, vocab_size).

idx_next = torch.multinomial(probs, num_samples=1) # (B, 1)

• Samples one token from the predicted probability distribution.
• Shape: (B, 1).

idx = torch.cat((idx, idx_next), dim=1) # (B, T+1)

• Appends the new token to the sequence.
• Sequence grows by one each loop.

return idx

• Returns the final generated sequence.

Summary of BigramLanguageModel

• __init__: builds the model (embeddings, blocks, head).
• forward: computes logits and (optional) loss.
• generate: produces new tokens step by step autoregressively.

Hpyerparameters

batch_size = 16  # number of sequences processed in parallel during training (mini-batch size)
block_size = 32  # maximum context length (number of tokens) the model looks back for prediction
max_iters = 5000  # total number of training iterations
eval_interval = 100  # how often (in iterations) to evaluate the model on validation set
learning_rate = 1e-3  # step size for optimizer updates (controls speed of learning)
device = 'cuda' if torch.cuda.is_available() else 'cpu'  # hardware to run training (GPU if available, else CPU)
eval_iters = 200  # number of batches to average over during evaluation
n_embd = 64  # dimensionality of token/position embeddings (hidden size of the model)
n_head = 4  # number of attention heads in each multi-head attention block
n_layer = 4  # number of stacked Transformer blocks
dropout = 0.0  # probability of randomly dropping units for regularization (0 means no dropout)
torch.manual_seed(1337)  # sets random seed for reproducibility of results

Training

The code trains a Transformer-based BigramLanguageModel to predict the next token in a sequence. During training, batches of data are passed through the model to compute logits and cross-entropy loss, and the optimizer updates parameters via backpropagation. Periodic evaluations track training and validation loss. Once trained, the model can generate new text by sampling tokens autoregressively from its learned probability distribution

model = BigramLanguageModel()
m = model.to(device)
# print the number of parameters in the model
print(sum(p.numel() for p in m.parameters())/1e6, 'M parameters')

# create a PyTorch optimizer
optimizer = torch.optim.AdamW(model.parameters(), lr=learning_rate)

for iter in range(max_iters):

    # every once in a while evaluate the loss on train and val sets
    if iter % eval_interval == 0 or iter == max_iters - 1:
        losses = estimate_loss()
        print(f"step {iter}: train loss {losses['train']:.4f}, val loss {losses['val']:.4f}")

    # sample a batch of data
    xb, yb = get_batch('train')

    # evaluate the loss
    logits, loss = model(xb, yb)
    optimizer.zero_grad(set_to_none=True)
    loss.backward()
    optimizer.step()

# generate from the model
context = torch.zeros((1, 1), dtype=torch.long, device=device)
print(decode(m.generate(context, max_new_tokens=2000)[0].tolist()))

1. Model & Optimizer Setup
   • Build BigramLanguageModel, move it to GPU/CPU.
   • Print number of parameters.
   • Create AdamW optimizer.
2. Training Loop
   • For each iteration (max_iters):
     • Evaluate loss on train/val sets every eval_interval.
     • Sample batch (xb, yb) of token sequences.
     • Forward pass: compute logits + loss.
     • Backward pass: zero grads → backprop → optimizer update.
3. Text Generation
   • Start with a seed token.
   • Use model to predict, sample, and append tokens autoregressively until max_new_tokens are generated.
   • Decode token IDs to readable text.

Output

Training process.

0.212567 M parameters
step 0: train loss 4.6484, val loss 4.6644
step 100: train loss 2.6778, val loss 2.6741
step 200: train loss 2.5182, val loss 2.5113
step 300: train loss 2.4330, val loss 2.4269
step 400: train loss 2.3646, val loss 2.3704
step 500: train loss 2.2988, val loss 2.3088
step 600: train loss 2.2665, val loss 2.2904
step 700: train loss 2.2275, val loss 2.2509
step 800: train loss 2.1749, val loss 2.1960
step 900: train loss 2.1445, val loss 2.1676
step 1000: train loss 2.1103, val loss 2.1306
step 1100: train loss 2.0764, val loss 2.1106
step 1200: train loss 2.0746, val loss 2.0989
step 1300: train loss 2.0440, val loss 2.0771
step 1400: train loss 2.0091, val loss 2.0518
step 1500: train loss 2.0004, val loss 2.0398
step 1600: train loss 1.9910, val loss 2.0241
step 1700: train loss 1.9635, val loss 2.0033
step 1800: train loss 1.9508, val loss 1.9992
step 1900: train loss 1.9326, val loss 1.9807
step 2000: train loss 1.9318, val loss 1.9672
step 2100: train loss 1.9180, val loss 1.9606
step 2200: train loss 1.8969, val loss 1.9454
step 2300: train loss 1.8943, val loss 1.9479
step 2400: train loss 1.8707, val loss 1.9362
step 2500: train loss 1.8756, val loss 1.9200
step 2600: train loss 1.8639, val loss 1.9207
step 2700: train loss 1.8561, val loss 1.9205
step 2800: train loss 1.8414, val loss 1.9121
step 2900: train loss 1.8317, val loss 1.8998
step 3000: train loss 1.8271, val loss 1.8965
step 3100: train loss 1.7993, val loss 1.8887
step 3200: train loss 1.8061, val loss 1.8762
step 3300: train loss 1.7893, val loss 1.8609
step 3400: train loss 1.7848, val loss 1.8660
step 3500: train loss 1.7719, val loss 1.8406
step 3600: train loss 1.7694, val loss 1.8632
step 3700: train loss 1.7737, val loss 1.8641
step 3800: train loss 1.7552, val loss 1.8575
step 3900: train loss 1.7428, val loss 1.8356
step 4000: train loss 1.7432, val loss 1.8500
step 4100: train loss 1.7295, val loss 1.8404
step 4200: train loss 1.7330, val loss 1.8404
step 4300: train loss 1.7155, val loss 1.8305
step 4400: train loss 1.7247, val loss 1.8546
step 4500: train loss 1.7141, val loss 1.8344
step 4600: train loss 1.7134, val loss 1.8373
step 4700: train loss 1.7056, val loss 1.8252
step 4800: train loss 1.6927, val loss 1.8178
step 4900: train loss 1.6920, val loss 1.8266
step 4999: train loss 1.6764, val loss 1.8028

Generated Poems

	 got like young on still Isavely,
Will eye? The sed, saw she was as all
Upos.—Her bevence, palled frelinence,
Of rived came fit
Fair from in shadels, reposoim dow
As than reprimes o'er for ear;—
Eveing when awbit his forther's sich dewems
Elympe the melf-sweeted find bell score! butchose but imatlently?
He me firce and breenely;
To the shendut and the mistring by,
He wrage; and once thealeling bassid's she wavel so know.
Thet her bell-limber'd eecrors slouble
Of sins forgerient twing, and straue,
Maden by this brsile had not. Say him it was of lid,
And elcause, Sast, she should knew our my dist a laofin gentlend immod;
Until-not in all peaceous soft two a trishe way
Of the moth us—now foot the love-brehail while in-dgid-will Aproar, which brise
As Cralmits formb'd one,—with she drillangerly and she fell.300
Ve drolong eyes did did,
Godwate, and fell with libors herres pread.
LV.
Then the wakes else
But in beheatain, gassuist, with sicalm;
So.—Hecheselines so pipent-feated, and the fair wreple dereemes323220
In eye, bend-catased me wondiar'd;
It thought down bow, look'f, before dowill caman drewhes,3—and all pass'd but a vercaus on a simel in the ride,
And give this, farerce resheace,
To shreet loay-gaven climb'd bourse all as she weep!
And were she slepost on in was, Fermehes, and foor.
These treepful form the tair thes swreak,
And the flewn with the tartle be ill forest when heard.
[51]
VII.
XI.
"O Fair voise,41ut at this threes
When glow'd holly treemess'd her arash
While delow, from the strain
One fair Jull flowine,
Thou arriend not me ashuls that said where Bolling sed in vate
The to did more shop could fair, their so will with side;
Not and fiere, my unsender-torous asweast?" deigh-wavery linger more,
Saw the proses, creal drowsing smet the night
Then these again, weepty to lise's
Astween-hise root bring anot a sudlemAng the water;
Thet not sideline a say he men Gods,
   Wherepet me aluded chapes of peees;
"brous'd-scarment'd harp her plantis,
My the tpise, sh

Links

Github

X

LinkendIn