Acrobot-ing with Actor Critic
The Acrobot environment is based on Sutton’s work in Generalization in Reinforcement Learning: Successful Examples Using Sparse Coarse Coding. The system consists of two links connected linearly to form a chain, with one end of the chain fixed. The joint between the two links is actuated. The goal is to apply torques on the actuated joint to swing the free end of the linear chain above a given height while starting from the initial state of hanging downwards.
For detail read: Acrobot.
Acrobot with Random Policy
import gym
import random
import time
#Episode ends when free end reaches target height
env = gym.envs.make("Acrobot-v1")
env.seed(786)
env.reset()
time.sleep(5)
state = env.reset()
is_done = False
total_reward_episode = 0
#the agent selecting action randomly
while not is_done:
env.render()
time.sleep(0.05)
action = random.choice([0, 1, 2])
next_state, reward, is_done, _ = env.step(action)
state = next_state
total_reward_episode += reward
print(total_reward_episode)
The Actor Critic Algorithm
The network for the actor-critic algorithm consists of the following two parts:
Actor: This takes in the input state and outputs the action probabilities.
Essentially, it learns the optimal policy by updating the model using information
provided by the critic.
Critic: This evaluates how good it is to be at the input state by computing the
value function. The value guides the actor on how it should adjust.
These two components share parameters of input and hidden layers in the network, as
learning is more efficient in this way than learning them separately. Accordingly, the loss
function is a summation of two parts, specifically, the negative log likelihood of action
measuring the actor, and the mean squared error between the estimated and computed
return measuring the critic.
Import all the necessary packages and create a Acrobot instance
import torch
import gym
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
import random
env = gym.make('Acrobot-v1')Actor Critic Neural Network Model
class ActorCriticModel(nn.Module):
def __init__(self, n_input, n_output, n_hidden):
super(ActorCriticModel, self).__init__()
self.fc = nn.Linear(n_input, n_hidden)
self.action = nn.Linear(n_hidden, n_output)
self.value = nn.Linear(n_hidden, 1)
def forward(self, x):
x = torch.Tensor(x)
x = F.relu(self.fc(x))
action_probs = F.softmax(self.action(x), dim=-1)
state_values = self.value(x)
return action_probs, state_valuesIn above class, the actor and critic share parameters of the input and the hidden
layers; the output of the actor consists of the probability of taking individual actions, and
the output of the critic is the estimated value of the input state.
The Policy Network
class PolicyNetwork():
def __init__(self, n_state, n_action, n_hidden=50, lr=0.001):
self.model = ActorCriticModel(n_state, n_action, n_hidden)
self.optimizer = torch.optim.Adam(self.model.parameters(), lr)
self.scheduler = torch.optim.lr_scheduler.StepLR(self.optimizer, step_size=10, gamma=0.9)
def predict(self, s):
"""
Compute the output using the Actor Critic model
@param s: input state
@return: action probabilities, state_value
"""
return self.model(torch.Tensor(s))
def update(self, returns, log_probs, state_values):
"""
Update the weights of the Actor Critic network given the training samples
@param returns: return (cumulative rewards) for each step in an episode
@param log_probs: log probability for each step
@param state_values: state-value for each step
"""
loss = 0
for log_prob, value, Gt in zip(log_probs, state_values, returns):
advantage = Gt - value.item()
policy_loss = -log_prob * advantage
value_loss = F.smooth_l1_loss(value, Gt)
loss += policy_loss + value_loss
self.optimizer.zero_grad()
loss.backward()
self.optimizer.step()
def get_action(self, s):
"""
Estimate the policy and sample an action, compute its log probability
@param s: input state
@return: the selected action, log probability, predicted state-value
"""
action_probs, state_value = self.predict(s)
action = torch.multinomial(action_probs, 1).item()
log_prob = torch.log(action_probs[action])
return action, log_prob, state_value
The Function implementing Actor-Critic
def actor_critic(env, estimator, n_episode, gamma=1.0):
"""
Actor Critic algorithm
@param env: Gym environment
@param estimator: policy network
@param n_episode: number of episodes
@param gamma: the discount factor
"""
for episode in range(n_episode):
log_probs = []
rewards = []
state_values = []
state = env.reset()
while True:
action, log_prob, state_value = estimator.get_action(state)
next_state, reward, is_done, _ = env.step(action)
total_reward_episode[episode] += reward
log_probs.append(log_prob)
state_values.append(state_value)
rewards.append(reward)
if is_done:
returns = []
Gt = 0
pw = 0
for reward in rewards[::-1]:
Gt += gamma ** pw * reward
pw += 1
returns.append(Gt)
returns = returns[::-1]
returns = torch.tensor(returns)
returns = (returns - returns.mean()) / (returns.std() + 1e-9)
estimator.update(returns, log_probs, state_values)
print('Episode: {}, total reward: {}'.format(episode, total_reward_episode[episode]))
if total_reward_episode[episode] >= 195:
estimator.scheduler.step()
break
state = next_state
Setting the parameters and hyperparameters and calling actor-critic function
#number of parameters in observation space of acrobot environment
n_state = env.observation_space.shape[0]
#number of actions the agent can take
n_action = env.action_space.n
#number of units of hidden layer
n_hidden = 500
#learning rate
lr = 0.003
#Instantiate the PolicyNetwork
policy_net = PolicyNetwork(n_state, n_action, n_hidden, lr)
#total number of episode to train the agent
n_episode = 1000
#discount rate
gamma = 0.9
#array to hold reward in each episode
total_reward_episode = [0] * n_episode
#calling the actor_critic function with above parameters and hyper parameters
#and training the agent
actor_critic(env, policy_net, n_episode, gamma)Plotting the Total Reward Gained in each episode
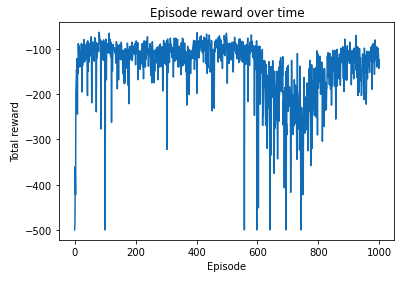
import matplotlib.pyplot as plt
plt.plot(total_reward_episode)
plt.title('Episode reward over time')
plt.xlabel('Episode')
plt.ylabel('Total reward')
plt.show()Output Figure
Testing the trained model for 100 episodes and calculating the average reward
episodes = 100
total_reward = []
total_positive_reward = []
count = 0
for episode in range(episodes):
print(episode)
state = env.reset()
is_done = False
total_reward_episode = 0
positive_reward_count = 0
while not is_done:
action, log_prob, state_value = policy_net.get_action(state)
next_state, reward, is_done, _ = env.step(action)
state = next_state
total_reward_episode += reward
if(reward > -1):
positive_reward_count += 1
#counting all episodes with total reward
if(total_reward_episode > -120):
count = count + 1
total_reward.append(total_reward_episode)
total_positive_reward.append(positive_reward_count)print(count)
print(sum(total_reward)/episodes)37
-137.6
Saving the model (Object of Policy Network) with Pickle
import pickle
def save_object(obj, filename):
with open(filename, 'wb') as outp:
pickle.dump(obj, outp, pickle.HIGHEST_PROTOCOL)
save_object(policy_net, 'actor_critic_acrobat.pkl')Putting All classes in single file so we can reuse them
Reloading the Trained Model and simulating
import gym
import torch
from collections import deque
import random
from nn_estimator import DQN
import pickle
import time
#need to import class of PolicyNetwork before importing its pickled object
#otherwise it will generate error
from PolicyNetwork_AC import PolicyNetwork
from PolicyNetwork_AC import ActorCriticModel
#Episode ends when free end reaches target height
env = gym.envs.make("Acrobot-v1")
env.seed(786)
env.reset()
time.sleep(5)
file_to_read = open("actor_critic_acrobat.pkl", "rb")
policy_net = pickle.load(file_to_read)
print(type(policy_net))
state = env.reset()
is_done = False
total_reward_episode = 0
while not is_done:
env.render()
time.sleep(0.05)
action, log_prob, state_value = policy_net.get_action(state)
next_state, reward, is_done, _ = env.step(action)
state = next_state
total_reward_episode += reward
print(total_reward_episode)