Balancing pole with Policy Gradient
The policy gradient algorithm trains an agent by taking small steps and updating the weight based on the rewards associated with those steps at the end of an episode.
The technique of having the agent run through an entire episode and then updating the policy based on the rewards obtained is called Monte Carlo policy gradient.
The action is selected based on the probability distribution computed based on the current state and the model’s weight.
For example, if the probabilities for the left and right actions are [0.6, 0.4], this means the left action is selected 60% of the time; it doesn’t mean the left action is chosen, as in the random search and hill-climbing algorithms.
We know that the reward is 1 for each step before an episode terminates for cartpole. Hence, the future reward we use to calculate the policy gradient at each step is the number of steps remaining.
After each episode, we feed the gradient history multiplied by the future rewards to update the weight using the stochastic gradient ascent method.
In this way, the longer an episode is, the bigger the update of the weight. This will eventually increase the chance of getting a larger total reward.
Information about cartpole of open ai gym
https://www.gymlibrary.ml/environments/classic_control/cart_pole/
Code of balancing the cartpole using the policy gradient
#import the basic libraries
import gym
import torchprint("The version of gym being used: ",gym.__version__)
print("The version of PyTorch being used: ",torch.__version__)The version of gym being used: 0.24.1
The version of PyTorch being used: 1.12.0+cu102
#making the cartpole environment
env = gym.make('CartPole-v1')#no of parameters in each state
#[Cart Position, Cart Velocity, Pole Angle, Pole Angular Velocity]
n_state = env.observation_space.shape[0]
#no of actions that can be taken
# 0 Push cart to the left
#1 Push cart to the right
n_action = env.action_space.n#this function simulates an episode given the input weight and returns the total reward and the gradients computed
def run_episode(env,weight):
#Reset the environment
state = env.reset()
#List to collect all the gradients in an episode
grads = []
total_reward = 0
is_done = False
while not is_done:
#converting the state from numpy to pytorch
state = torch.from_numpy(state).float()
#Multiply state with the weight
z = torch.matmul(state,weight)
#Calculates the probabilities, probs , for both actions based on the #current state and input weight
probs = torch.nn.Softmax()(z)
#Take an action based on the probability
action = int(torch.bernoulli(probs[1]).item())
#Obtain the derivative of softmax function
d_softmax = torch.diag(probs) - probs.view(-1,1)*probs
#Obtain log term with respect to policy
d_log = d_softmax[action]/probs[action]
#Calculate the gradient
grad = state.view(-1,1)*d_log
#Collect the gradient
grads.append(grad)
#find the reward and next state by taking the action
state,reward,is_done,_ = env.step(action)
#Add the total reward of the episode
total_reward += reward
#If the episode is completed break the loop
if is_done:
break
#Return total reward and gradients obtained from this episode
return total_reward,grads
#Random seed
random_seed = 1
torch.manual_seed(random_seed)weight = torch.rand(n_state,n_action)
total_reward,gradients = run_episode(env,weight)
print(total_reward)
#Random weight to get start wirh
weight = torch.rand(n_state,n_action)
total_rewards = []
learning_rate = 0.001
episode = 1
while True:
total_reward,gradients = run_episode(env,weight)
print('Episode {}:{}'.format(episode+1,total_reward))
#updating the weight
for i,gradient in enumerate(gradients):
weight += learning_rate*gradient * (total_reward - i)
total_rewards.append(total_reward)
episode += 1
#If we get more than 200 of last 100 episode then we assume the training has been completed
if episode >= 99 and sum(total_rewards[-100:])/100 >= 450:
break
print("The agent was trained in {} episodes".format(episode))
print('The Average total reward over {} episode: {}'.format(episode,sum(total_rewards)/episode))
The agent was trained in 441 episodes
The Average total reward over 441 episode: 240.25850340136054
import matplotlib.pyplot as plt
plt.figure(figsize=(10,7))
plt.plot(total_rewards)
plt.title('Rewards in each episode')
plt.xlabel('Episode')
plt.ylabel('Reward')
plt.show()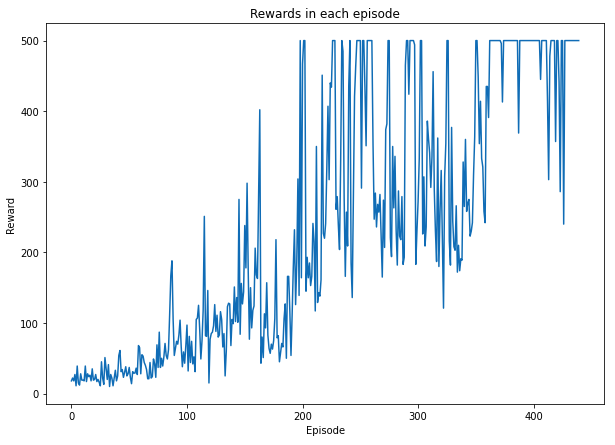
#Evaluation of final weight obtained using Policy Gradient
n_episode_eval = 100
total_rewards_eval = []
for episode in range(n_episode_eval):
total_reward,_ = run_episode(env,weight)
print('Episode {}:{}'.format(episode+1,total_reward))
total_rewards_eval.append(total_reward)
print('The Average total reward over {} episode: {}'.format(n_episode_eval,sum(total_rewards_eval)/n_episode_eval))
The Average total reward over 100 episode: 500.0