Q-Taxi
Introduction
There are four designated locations in the grid world indicated by R(ed), G(reen), Y(ellow), and B(lue). When the episode starts, the taxi starts off at a random square and the passenger is at a random location. The taxi drives to the passenger’s location, picks up the passenger, drives to the passenger’s destination (another one of the four specified locations), and then drops off the passenger. Once the passenger is dropped off, the episode ends.
https://www.gymlibrary.ml/environments/toy_text/taxi/
Actions
There are 6 discrete deterministic actions:
- 0: move south
- 1: move north
- 2: move east
- 3: move west
- 4: pickup passenger
- 5: drop off passenger
Observations
There are 500 discrete states since there are 25 taxi positions, 5 possible locations of the passenger (including the case when the passenger is in the taxi), and 4 destination locations.
Note that there are 400 states that can actually be reached during an episode. The missing states correspond to situations in which the passenger is at the same location as their destination, as this typically signals the end of an episode. Four additional states can be observed right after a successful episodes, when both the passenger and the taxi are at the destination. This gives a total of 404 reachable discrete states.
Each state space is represented by the tuple: (taxi_row, taxi_col, passenger_location, destination)
An observation is an integer that encodes the corresponding state. The state tuple can then be decoded with the “decode” method.
Passenger locations:
- 0: R(ed)
- 1: G(reen)
- 2: Y(ellow)
- 3: B(lue)
- 4: in taxi
Destinations:
- 0: R(ed)
- 1: G(reen)
- 2: Y(ellow)
- 3: B(lue)
Rewards
- -1 per step unless other reward is triggered.
- +20 delivering passenger.
- -10 executing “pickup” and “drop-off” actions illegally.
Basic Code
import gym
import time
render_time = 10
#initialize the enviroment
env = gym.make('Taxi-v3')
#Get state
state = env.reset()
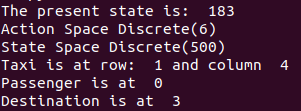
print("The present state is: ",state)
#Render the environment
env.render()
time.sleep(render_time)
#Total possible action
print("Action Space {}".format(env.action_space))
#Total possible observation space
print("State Space {}".format(env.observation_space))
#Position of taxi, customer and destination
taxi_row, taxi_col, passenger_index, destination_index = env.decode(state)
print('Taxi is at row: ',taxi_row,'and column ',taxi_col )
print('Passenger is at ',passenger_index)
print('Destination is at ',destination_index)Output

Choosing an action manually

env.step(1) #going north
print(state)
env.render()
time.sleep(render_time)
Setting a state manually
print('Setting a state manually')
state = env.reset()
env.env.s = 20
env.render()
time.sleep(render_time)
Code for taking random actions and trying to achieve the goal
import time
import gym
import numpy as np
from matplotlib import pyplot as plt
from matplotlib.pyplot import figure
#initialize the enviroment
env = gym.make('Taxi-v3')
episodes = 5000
the_rewards = []
the_epochs = []
for episode in range(episodes):
state = env.reset()
#env.render()
episode_reward = 0
epochs = 0
reward = 0
while reward != 20:
observation,reward,done,info = env.step(env.action_space.sample())
episode_reward = episode_reward + reward
epochs += 1
the_rewards.append(episode_reward)
the_epochs.append(epochs)
#if average reward for 50 episodes is greater than zero and average time steps for 50 episodes is less than 20
#We assume that saturation has been reached
if((np.mean(the_rewards[-50:]) > 0) and (np.mean(the_epochs[-50:]) < 20) ) :
break
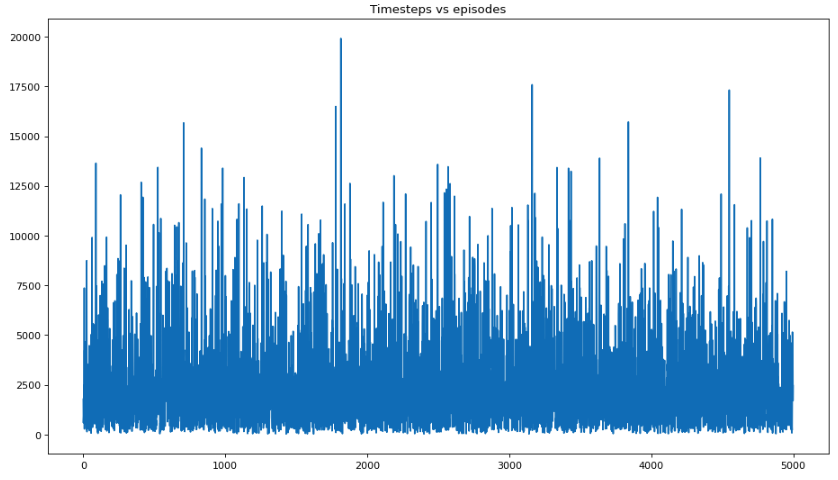
print("Average reward per episdoe: {}".format(np.sum(the_rewards)/len(the_rewards)))
print("Average epoch per episdoe: {}".format(np.sum(the_epochs)/len(the_epochs)))
figure(figsize=(14,8), dpi=80)
plt.plot(the_rewards)
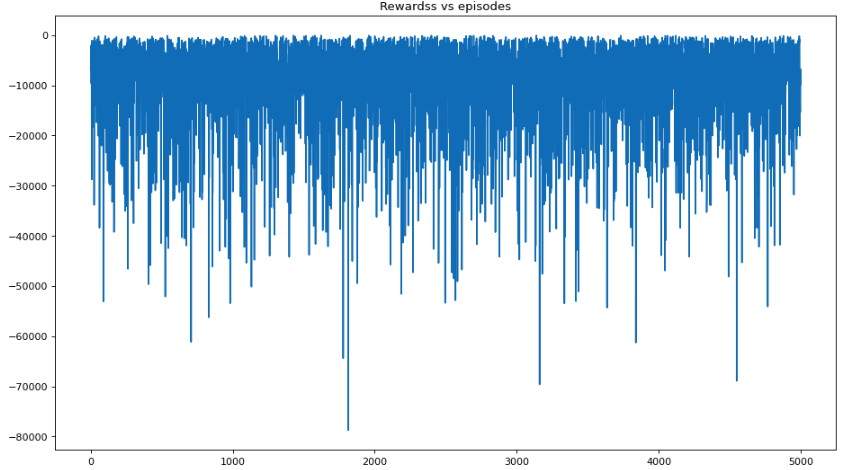
plt.title("Rewardss vs episodes")
plt.show()
figure(figsize=(14,8), dpi=80)
plt.plot(the_epochs)
plt.title("Timesteps vs episodes")
plt.show()Average reward per episode: -9548.2424
Average epoch per episode: 2444.3888
Q-learning
The following code tries to improve the performance of the agent with the help of Q-learning.
import gym
import numpy as np
import time
from matplotlib import pyplot as plt
from matplotlib.pyplot import figure
render_time = 0.5
env = gym.make('Taxi-v3')
state = env.reset()
episodes = 6000
#Creating Q-table
Q = np.zeros([env.observation_space.n,env.action_space.n])
#set hyperparameters
gamma = 0.1
alpha = 0.1
the_rewards = []
the_timestep = []
for episode in range(episodes):
timestep = 0
reward = 0
episode_reward = 0
#initialize Environment
state = env.reset()
#create update loop
while reward !=20:
#Choosing action greedily for the given state
action = np.argmax(Q[state])
#The new observations after taking the action
next_state,reward,done,info = env.step(action)
#Updating the Q-value for particular state-action pair using the Bellman Equation
Q[state,action] = Q[state,action] + alpha * (reward + gamma * np.max(Q[next_state]) - Q[state,action])
#Setting the present state as the new state
state = next_state
#Increasing the count of timestep
timestep += 1
episode_reward = episode_reward + reward
the_rewards.append(episode_reward)
the_timestep.append(timestep)
#if average reward for 50 episodes is greater than zero and average time steps for 50 episodes is less than 20
#We assume that saturation has been reached
if((np.mean(the_rewards[-50:]) > 0) and (np.mean(the_timestep[-50:]) < 20)) :
print('Saturation at {}'.format(episode))
break
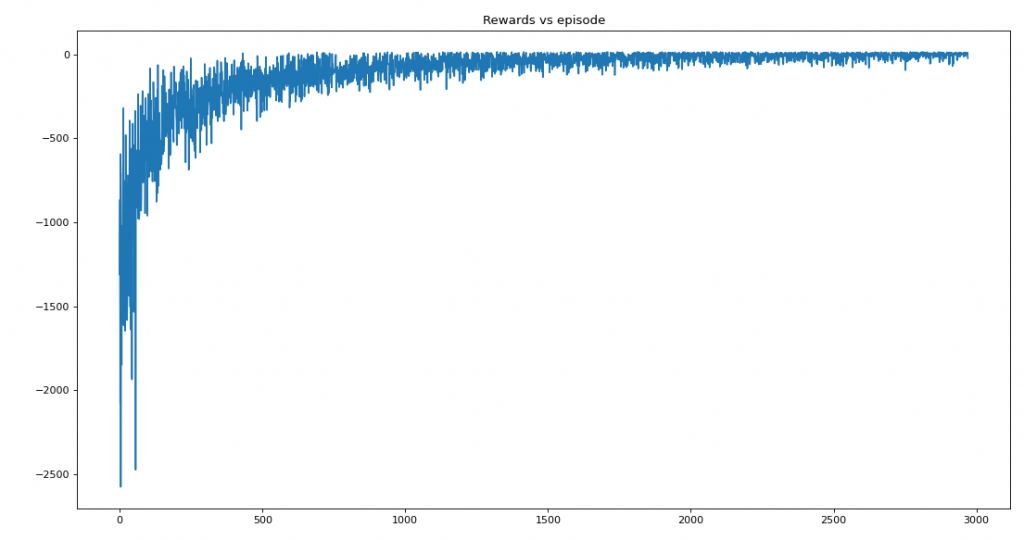
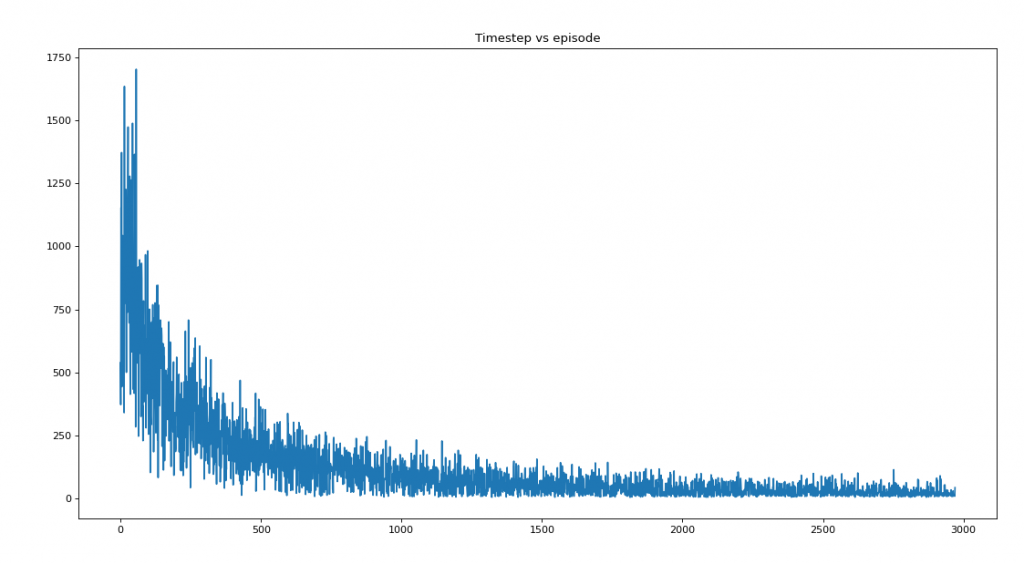
print("Average reward per episdoe: {}".format(np.sum(the_rewards)/len(the_rewards)))
print("Average timesteps per episdoe: {}".format(np.sum(the_timestep)/len(the_timestep)))
figure(figsize=(14,8), dpi=80)
plt.plot(the_rewards)
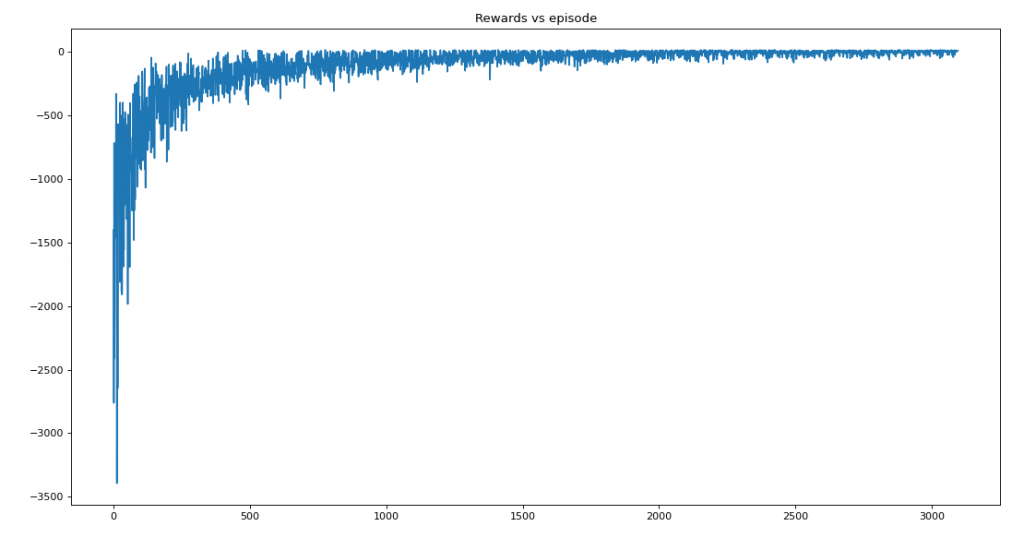
plt.title('Rewards vs episode')
plt.show()
figure(figsize=(14,8), dpi=80)
plt.plot(the_timestep)
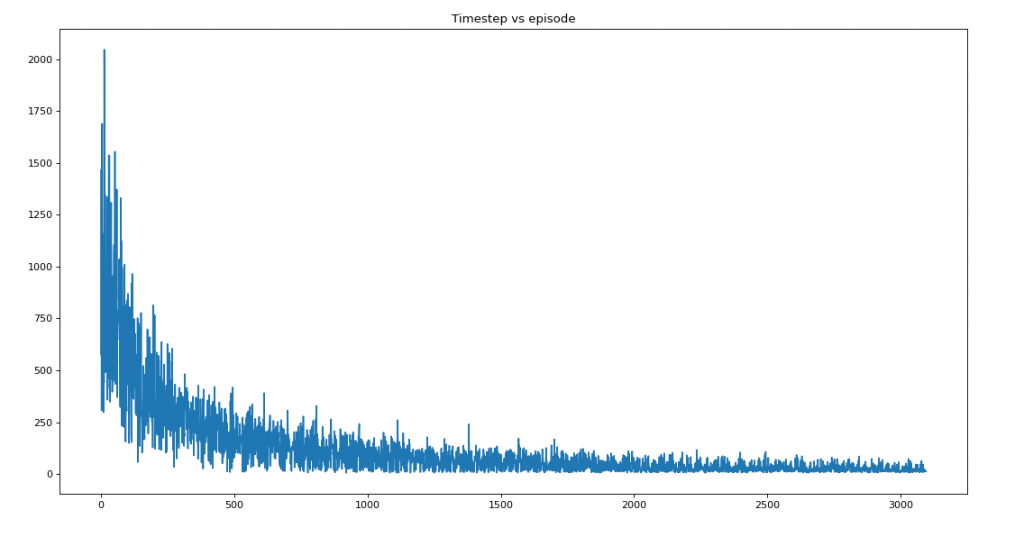
plt.title('Timestep vs episode')
plt.show()Saturation at 2970
Average reward per episode: -100.91787277011107
Average timesteps per episode: 117.34365533490407
Q-Learning with epsilon greedy
This method explores 10% of time and remains greedy 90% of time.
import gym
import numpy as np
import time
from matplotlib import pyplot as plt
from matplotlib.pyplot import figure
render_time = 0.5
env = gym.make('Taxi-v3')
state = env.reset()
episodes = 6000
Q = np.zeros([env.observation_space.n,env.action_space.n])
#set hyperparameters
gamma = 0.1
alpha = 0.1
epsilon = 0.1
#the_rewards = np.zeros([episodes,1])
the_rewards = []
the_timestep = []
for episode in range(episodes):
timestep = 0
reward = 0
episode_reward = 0
#initialize Environment
state = env.reset()
#create update loop
while reward !=20:
if np.random.rand() < epsilon:
#exploration option
action = env.action_space.sample()
else:
#exploitation option
action = np.argmax(Q[state])
next_state,reward,done,info = env.step(action)
Q[state,action] = Q[state,action] + alpha * (reward + gamma * np.max(Q[next_state]) - Q[state,action])
state = next_state
timestep += 1
episode_reward = episode_reward + reward
the_rewards.append(episode_reward)
the_timestep.append(timestep)
#if average reward for 50 episodes is greater than zero and average time steps for 50 episodes is less than 20
#We assume that saturation has been reached
if((np.mean(the_rewards[-50:]) > 0) and (np.mean(the_timestep[-50:]) < 20) ) :
print('Saturation at {}'.format(episode))
break
env.render()
time.sleep(render_time)
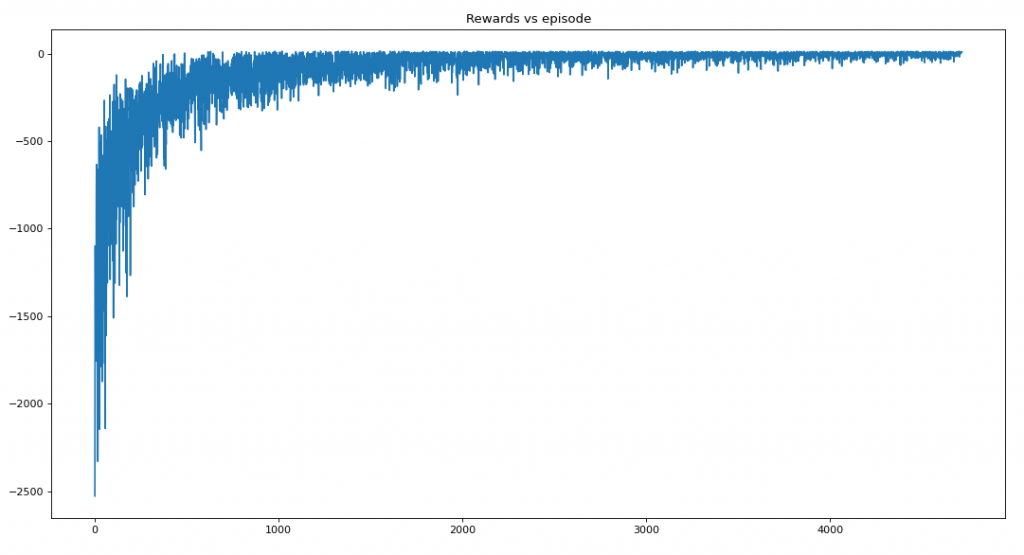
print("Average reward per episdoe: {}".format(np.sum(the_rewards)/len(the_rewards)))
print("Average timesteps per episdoe: {}".format(np.sum(the_timestep)/len(the_timestep)))
figure(figsize=(14,8), dpi=80)
plt.plot(the_rewards)
plt.title('Rewards vs episode')
plt.show()
figure(figsize=(14,8), dpi=80)
plt.plot(the_timestep)
plt.title('Timestep vs episode')
plt.show()
Saturation at 4718
Average reward per episode: -90.01356219538037
Average timesteps per episode: 84.84700148336512
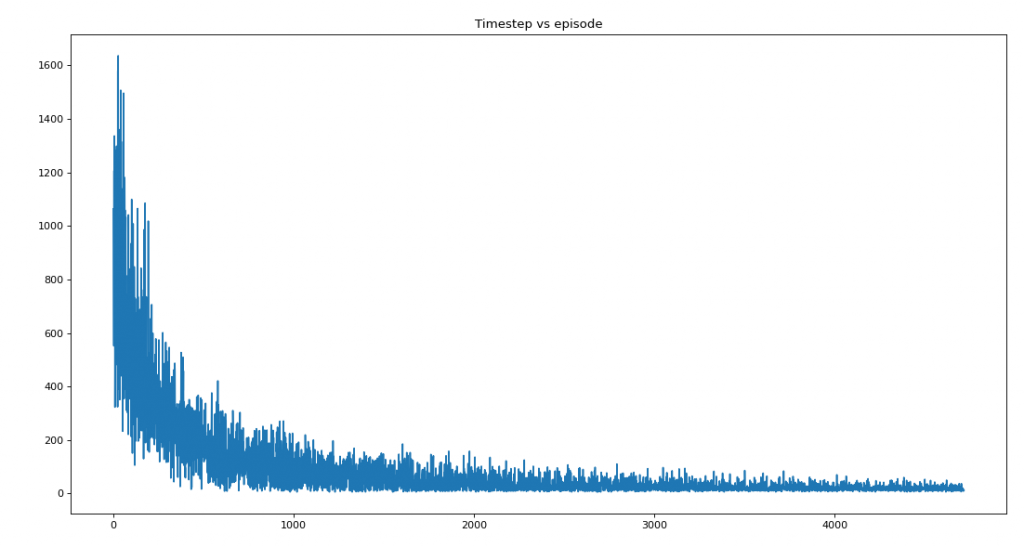
Q Learning with Decaying Epsilon
The agent explores less as it gains the knowledge about the environment
import gym
import numpy as np
import time
from matplotlib import pyplot as plt
from matplotlib.pyplot import figure
render_time = 0.5
env = gym.make('Taxi-v3')
state = env.reset()
episodes = 6000
Q = np.zeros([env.observation_space.n,env.action_space.n])
#set hyperparameters
gamma = 0.1
alpha = 0.1
epsilon = 0.1
epsilon_decay = 0.99
#the_rewards = np.zeros([episodes,1])
the_rewards = []
the_timestep = []
for episode in range(episodes):
timestep = 0
reward = 0
episode_reward = 0
epsilon = epsilon * epsilon_decay
#initialize Environment
state = env.reset()
#create update loop
while reward !=20:
if np.random.rand() < epsilon:
#exploration option
action = env.action_space.sample()
else:
#exploitation option
action = np.argmax(Q[state])
next_state,reward,done,info = env.step(action)
Q[state,action] = Q[state,action] + alpha * (reward + gamma * np.max(Q[next_state]) - Q[state,action])
state = next_state
timestep += 1
episode_reward = episode_reward + reward
the_rewards.append(episode_reward)
the_timestep.append(timestep)
#if average reward for 50 episodes is greater than zero and average time steps for 50 episodes is less than 20
#We assume that saturation has been reached
if((np.mean(the_rewards[-50:]) > 0) and (np.mean(the_timestep[-50:]) < 20) ) :
break
print('Saturation at {}'.format(episode))
env.render()
time.sleep(render_time)
print("Average reward per episdoe: {}".format(np.sum(the_rewards)/len(the_rewards)))
print("Average timesteps per episdoe: {}".format(np.sum(the_timestep)/len(the_timestep)))
figure(figsize=(14,8), dpi=80)
plt.plot(the_rewards)
plt.title('Rewards vs episode')
plt.show()
figure(figsize=(14,8), dpi=80)
plt.plot(the_timestep)
plt.title('Timestep vs episode')
plt.show()Saturation at 3096
Average reward per episode: -101.80787859218599
Average timesteps per episode: 114.07523409751373